2015-07-14
646
3.1. Определите, при каких значениях параметра m прямая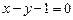 
является касательной к графику функции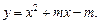 
3.2. К графику функции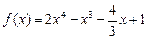 
в точке 
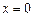проведена касательная. Найдите расстояние от начала координат до этой касательной.
3.3. К графику функции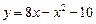 
проведены две касательные. Первая проводится в точке с абсциссой 
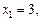а вторая – в точке, ордината которой равна 6. Найдите площадь треугольника, образованного этими касательными и осью ординат.
3.4. Прямая пересекает параболу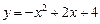 
в двух точках 
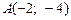и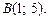 
Напишите уравнение касательной к параболе, параллельной этой секущей. Найдите угол, под которым нормаль, проведенная в точку касания, пересекает ось абсцисс.
3.5. Движения двух материальных точек по одной прямой заданы уравнениям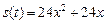и 
и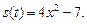 
Найдите скорости движения точек в те моменты, когда пройденные ими расстояния равны.
3.6. Масса неоднородного стержня длины l вычисляется по формуле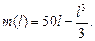 
Определите, при каком значении l плотность стержня будет втрое меньше, чем в начале стержня.
