1.1.Определение первообразной. Неопределенный интеграл и его свойства. Интегралы от элементарных функций.
Первообра́зной данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Неопределенным интегралом 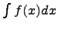 называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равен подынтегральному выражению f(x)dx, т.е.
называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равен подынтегральному выражению f(x)dx, т.е. 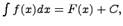 или
или 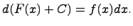 Функцию F(x) называют первообразной функции f(x). Первообразная функции f(x) определяется с точностью до постоянной величины.
Функцию F(x) называют первообразной функции f(x). Первообразная функции f(x) определяется с точностью до постоянной величины.
Свойства неопределённого интеграла:
Если функция f (x) имеет первообразную на промежутке X, и k – число, то 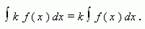 Короче: постоянную можно выносить за знак интеграла.
Короче: постоянную можно выносить за знак интеграла.
Если функции f (x) и g (x) имеют первообразные на промежутке X, то 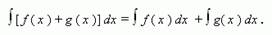 Короче: интеграл суммы равен сумме интегралов.
Короче: интеграл суммы равен сумме интегралов.
Если функция f (x) имеет первообразную на промежутке X, то для внутренних точек этого промежутка: 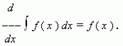 Короче: производная от интеграла равна подынтегральной функции.
Короче: производная от интеграла равна подынтегральной функции.
Если функция f (x) непрерывна на промежутке X и дифференцируема во внутренних точках этого промежутка, то: 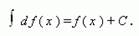
Короче: интеграл от дифференциала функции равен этой функции плюс постоянная интегрирования.
Интегралы от элементарных функций:
Некоторые приемы интегрирования: замена переменной; интегрирование по частям; интегрирование дроби, знаменатель который является квадратным трехчленом; интегрирование выражений, содержащих тригонометрические функции.
Формула замены переменной. Пусть имеет смысл сложная функция 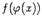 , где Х изменяется на некотором интервале. Тогда
, где Х изменяется на некотором интервале. Тогда 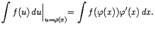 (1.3)
(1.3)
(В левой части после вычисления интеграла 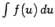 сделана подстановка
сделана подстановка 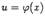 .) Для доказательства обозначим через F(u) некоторую первообразную для f(u) и через G(x) -- первообразную для
.) Для доказательства обозначим через F(u) некоторую первообразную для f(u) и через G(x) -- первообразную для 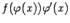 . Это означает, что
. Это означает, что 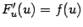 и
и 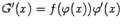 . Доказываемое равенство (1.3) эквивалентно тогда такому:
. Доказываемое равенство (1.3) эквивалентно тогда такому: 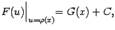 или
или 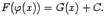 Для доказательства последнего соотношения достаточно проверить. что совпадают производные левой и правой частей. Но по формуле производной сложной функции получаем:
Для доказательства последнего соотношения достаточно проверить. что совпадают производные левой и правой частей. Но по формуле производной сложной функции получаем: 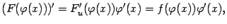 то есть то же, что и
то есть то же, что и 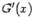 . Формула (1.3) доказана. Заметим, что выражение
. Формула (1.3) доказана. Заметим, что выражение 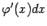 в правой части (1.3) есть не что иное, как дифференциал du(x) функции. Так что мы можем записать (1.3) в виде
в правой части (1.3) есть не что иное, как дифференциал du(x) функции. Так что мы можем записать (1.3) в виде 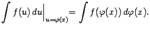
Теперь, после этого доказательства, мы получили право трактовать в обозначении неопределённого интеграла как некоторый дифференциал, а не просто как элемент обозначения интеграла, вроде скобки.
Формула интегрирования по частям. Пусть функции f(x) и g(x) имеют производную на рассматриваемом интервале изменения x. Тогда верно равенство 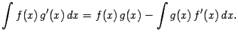 (1.5) Эта формула называется формулой интегрирования по частям. Она позволяет "перебрасывать" производную с функции g(x), стоящей под знаком интеграла, на другой подынтегральный множитель f(x). При этом в правой части равенства появляется внеинтегральный член f(x)g(x).
(1.5) Эта формула называется формулой интегрирования по частям. Она позволяет "перебрасывать" производную с функции g(x), стоящей под знаком интеграла, на другой подынтегральный множитель f(x). При этом в правой части равенства появляется внеинтегральный член f(x)g(x).
Пусть F(x) -- первообразная для 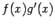 и G(x) -- первообразная для
и G(x) -- первообразная для 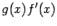 . Тогда равенство (1.5) можно записать в виде
. Тогда равенство (1.5) можно записать в виде 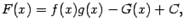
где G-- некоторая постоянная. Докажем, что производные левой и правой частей совпадают. По определению, 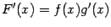 . С другой стороны,
. С другой стороны, 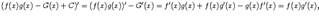
то есть производные совпадают, и формула (1.5) доказана. Мы видим, что она является следствием формулы для производной произведения.
Вводя обозначения 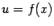 и
и 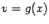 и замечая, что
и замечая, что 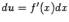 и
и 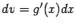 , мы можем записать формулу интегрирования по частям в виде
, мы можем записать формулу интегрирования по частям в виде 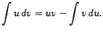 .
.
Интегрирование рациональных дробей:
Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов. Сам метод заключается в разложении рациональной дроби на сумму простейших дробей. Всякую правильную рациональную дробь 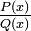 , знаменатель которой разложен на множители
, знаменатель которой разложен на множители 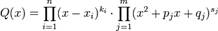
можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:
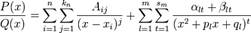
где Aij,αlt,βlt — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.
Интегрирование тригонометрических функций:
1°. Интегралы вида
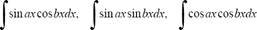
находятся с помощью тригонометрических формул
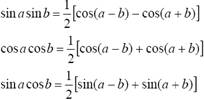
2°. Интегралы вида
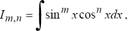
где m и n - четные числа находятся с помощью формул понижения степени
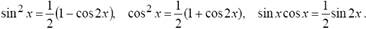
Если хотя бы одно из чисел m или n - нечетное, то полагают (пусть m = 2k + 1)
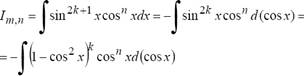
3°. Если m = -m, n = -l - целые отрицательные числа одинаковой четности, то 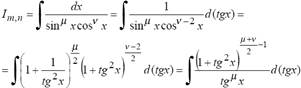
В частности, к этому случаю сводятся интегралы 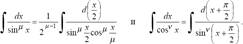
4°. Интегралы вида
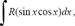
где R - рациональная функция от sinx и cosx, приводятся к интегралам от рациональных функций новой переменной с помощью подстановки 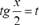 при этом
при этом 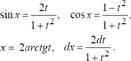
Если R{-sin x, cosx) = R(sinx, cosx), то целесообразно применить подстановку tgx = t. при этом 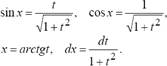
 2015-08-12
2015-08-12 1124
1124