| ВЫПУСК | |||||
| затраты | i | 1.Отражает промежуточное потребление x – промежуточное потребление 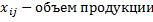 , , 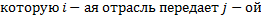 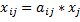 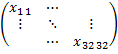 | 2.Отражает конечное потребление 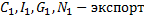 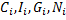 | 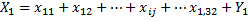 … … 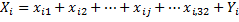 … … 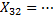 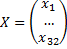 - промежуточное потребление - промежуточное потребление 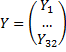 - вектор конечных выпусков - вектор конечных выпусков 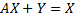 – выпуск – выпуск 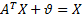 – затраты – затраты | |
| i | |||||
| … | |||||
| … | |||||
| i | |||||
| … | |||||
| … | |||||
| … | |||||
| … | |||||
| … | |||||
| … | |||||
| … | |||||
| i | |||||
| … | |||||
| … | |||||
| 32 | |||||
3.Добавленная стоимость, налоги, импорт 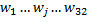 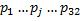 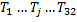 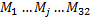 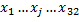 | 4. Перерас-пределение националь-ного продукта | 1+2 | 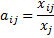 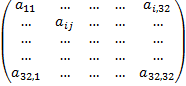 - матрица отраслевой структуры экономики - матрица отраслевой структуры экономики   | ||
| 1+3 | = |
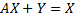
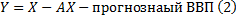
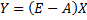
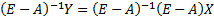
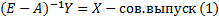
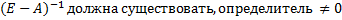
Матрица полных затрат существует тогда и только тогда, когда максимальное собственное значение матрицы A<1 (матрица продукта)
Главная задача – планирование рациональной структуры ВВП
(4) Модель межотраслевого баланса позволяет анализировать отраслевую структуру экономики (матрицу А) и использовать её для текущего планирования.
Разрабатывается динамичная модель межотраслевого баланса (для средне- и долгосрочного планирования)
(3) 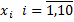 ;
; 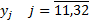
(5) В модели выбираем оптимальный план с учетом эффективности экономического роста.
| С/х | Промышленность | Услуги | Конечный спрос (У) | Валовой | |
| С/х | |||||
| Промышленность | |||||
| Услуги |
Матрица коэффициентов
ЗАДАЧА
Динамическая модель:
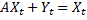
Чтобы в явном виде был виден воспроизводственный процесс, то переписываем балансовое уравнение как:
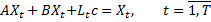
A – матрица коэффициентов прямых затрат
B – матрица фондоёмкости
Lt – численность занятых
с – уровень потребления на одного занятого
Рассмотрение 33ей отрасли – трудовые ресурсы.
3. Модель международной торговли
Матричная модель – структурная матрица, только в ней отражаются потоки экспорта и импорта.
Матрица для торговых партнеров: n=n.
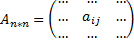
По горизонтали – импортеры.
По вертикали – экспортеры.
Торговые бюджеты – вектор X:
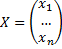
Aij отражает часть торгового бюджета j-ой страны идущей на импорт из i-ой страны
Экспорт должен быть равен импорту, что и будет показывать сбалансированность.
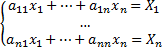
Обязательное правило: все торговые бюджеты распределяются на внутреннее потребление и импорт.
В матрично-векторном виде, то же самое получаем как: AX=X
Eigenvals(A), eigenvecs(A;1,5) = X – в MathCad, где 1,5 – это лямбда.
Т.о. AX = 1,5 *X
Если 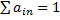 сумма по столбцам равна единице, т.е. сбалансировано, тогда существует максимальное лямбда a равное единице. Значения в матрице по диагонали показывают как страна торгует сама с собой.
сумма по столбцам равна единице, т.е. сбалансировано, тогда существует максимальное лямбда a равное единице. Значения в матрице по диагонали показывают как страна торгует сама с собой.
11. Современные модели экономического развития и роста
1. Производственные функции и их свойства
Производственная функция выражает зависимость результата производства от затрат ресурсов.
Ресурсы – труд и капитал:
K, L → Y
Капитал – основные производственные фонды.
Труд измеряется-рассматривается численность занятых в экономике, можно человеко-часы (на микроуровне).
Производственная функция может быть представлена в различной форме: Y=F(K,L). Такая функция называется неоклассической если является гладкой и удовлетворяет условиям:
1. При отсутствии одного из ресурсов производство невозможно: F(0,L)=F(K,0)=0
2. С ростом ресурсов выпуск растет: 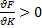 ,
, 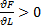
3. С ростом ресурсов скорость выпуска замедляется: вторые производные отрицательные.
4. При неограниченном увеливении одного из ресурса, выпуск неограниченно растет: F(+бесконечность;L)=F(K;+бесконечность)=+бесконечность
Функция Коба-Дугласа: 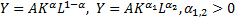 .
.
Параметр А – нейтральный технический прогресс. Оцениваются такие функции эконометрическими метода, логарифмируются, приводятся к лобно-линейной множественной регрессии, приведение к виду по МНК.
Частные первые производные:

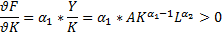
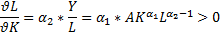
Интерпретация параметров:
Альфа 1 – эластичность выпуска по капиталу, альфа 2 – по труду.
Если: 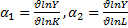
Альфа 1 больше альфа – трудосберегающий рост, наоборот – фондосберегающий.
Фондосберегаеющий – экстенсивный рост, наоборот – интенсивный
Альфа 1 примерно 1/3, для развитых стран ½, у нас альфа 1 = 2/3, т.к. у нас доля капитала в выпуске 68%, труда – 32%.
Изокванты – это линии или множество точек в плоскости, для которых выполняется соотношение F(K,L)=Y0 - константа.
Изоклинии показывают возможности максимального роста производственной фнкции. Это ортогоналдьна изокванте:
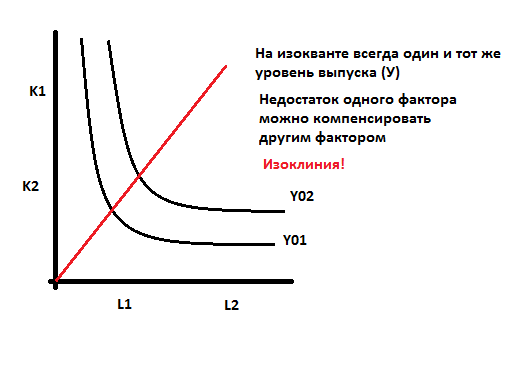
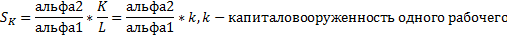
Предельная норма замены труда фондами
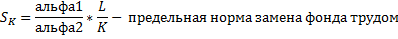
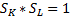
Выражение одного параметра (роста) от другого., масштаб и эффективность производства:
В индексной форме:
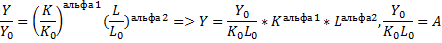
Соизмеряется ресурсы с выпуском в базисном году – А.
Эффективность:

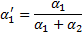
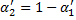
Масштаб:
Темп роста выпуска (Y c волной)=E*M
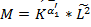
Производственная функция для США: Y=2,248*K0,404*L803
А – в 2,248 раза выпуск в году превышал объем затраченный ресурсов.
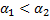 – фондосберегающий рост, с увеличение производственных фондов на 1% выпуск вырастет на 0,4%, трудовые – 0,8%.
– фондосберегающий рост, с увеличение производственных фондов на 1% выпуск вырастет на 0,4%, трудовые – 0,8%.
ВВП США вырос в 2,82 раза с 1960-ого года. Это означает, что Y с волной = 2,82. K с чертой = 2,88. Численность занятых увеличилось в 1,93 раза, L с чертой = 1,93. За счет чего вырос ВВП в 2,82 раза?
Эффективность:
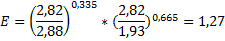
Масштаб:
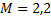
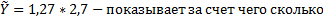
Однородная функция степени Гамма, если 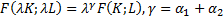 .
.
Частные функции Коба-Дугласа:
· Линейная: Y=AK+BL
· Функция Леонтьева: 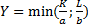
· 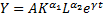 рассматривает инновационный прогресс. Искусственная функция.
рассматривает инновационный прогресс. Искусственная функция.
2. Равновесные динамические макромодели
Модель Солоу (саморегулирующийся рынок, важный фактор – труд).
Предпосылки:
· убывающая производительность капитала (фондоотдача)
· постоянная отдача от масштаба
· неизменная норма выбытия
· отсутствие инвестиционных лагов
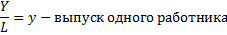
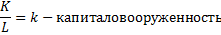
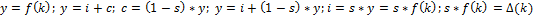
Отсюда находится равновесный уровень капиталовооруженности.
Проблема базовой модели Солоу: модель не объясняет механизм экономического роста (каким образом происходит увеличение); возникает проблема сходимости (достижения равновесного уровня) для различных стран (развивающихся, развитых).
Добавляются новые параметры:
n - темп роста населения
g - темп роста НТП
Направления развития модели Солоу:
 2015-08-13
2015-08-13 851
851








