Определение криволинейного интеграла первого рода

Рассмотрим пространственную кусочно-гладкую кривую, ограниченную точками А и В (рисунок 7.12), и определенную на ней непрерывную функцию f (x; y; z) = f (M), где М (х; у; z) – точка кривой. Дугу АB разобьем точками M ₁, M ₂,…, М_{п –1} на n элементарных дуг М_{i‑ 1} М_i, (i = 1,2,…, п; M _o = А; М_п = В), длины которых обозначим соответственно D l ₁, D l ₂,…, D l_п, а наибольшую из этих длин – l. На каждой из элементарных дуг M_{i– 1} M_i выберем произвольно одну точку М_i ¢(х_i ¢; y_i ¢; z_i ¢) и составим сумму

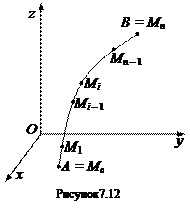
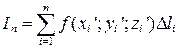, (7.14)

называемую интегральной суммой для функции f (x; у; z) пo длине дуги кривой AB.

Криволинейным интегралом первого рода от функции f (x; у; z) по кривой АВ называется предел интегральной суммы (7.14) при l ® 0:

.

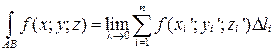На кривой АВ, целиком лежащей на плоскости Оху, функция f от координаты z не зависит, поэтому по определению имеем

.

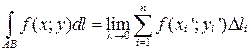Если подынтегральную функцию f (x; у; z) > 0 рассматривать как линейную плотность кривой АВ, то криволинейный интеграл первого рода представляет собой массу этой кривой.

7.8 ОПРЕДЕЛЕНИЕ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА
ВТОРОГО РОДА

Пусть дана дуга пространственной кусочно-гладкой кривой, ограниченная точками А и В (см. рисунок 7.12), и определенная на ней непрерывная вектор-функция

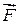(x; у; z) = Р (х; у; z) i + Q (x; у; z) j + R (х; у; z) k. (7.15)

Дугу АВ разобьем на п элементарных дуг M_{i– 1} M_i (i = 1;2;..., п; M_o = А; M_п = В) точками M ₁(x ₁; y ₁;z₁), M ₂(х ₂; у ₂; z ₂),..., M_{n -1}(x_{n -1}; у_{п -1}; z_{n -1}). На каждой дуге M_{i– 1} M_i выберем произвольно одну точку M¢_i (x¢_i; y¢_i; z¢_i); значения функций Р (x¢_i; y¢_i; z¢_i) = Р (М¢_i), Q (x¢_i; y¢_i; z¢_i) = Q (M¢_i), R (x¢_i; y¢_i; z¢_i) = R (M¢_i) в этой точке умножим на проекции данной дуги соответственно на оси Ох, Оу, Оz, которые обозначим через D x_i, D y_i, D z_i, причем D x_i = x_i – x_{i– 1}, D y_i = y_i – y_{i– 1}, D z_i = z_i – z_{i– 1}. Из полученных произведений составим сумму

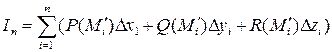, (7.16)

называемую интегральной суммой по координатам для вектор-функции (7.15). Обозначим через l длину наибольшей из проекций D x_i, D y_i, D z_i.

Криволинейным интегралом второго рода, взятым по кривой L или по пути АВ, называется предел интегральной суммы (7.16) при l ® 0:

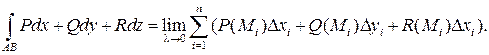
На кривой L, целиком лежащей в плоскости Оху, функции Р, Q, R не зависят от z, D z_i = 0, dz = 0, поэтому

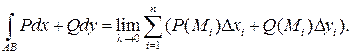
Если функции Р, Q, R рассматривать как проекции некоторой переменной силы на координатные оси, то криволинейный интеграл второго рода выражает работу силы (Р, Q, R), точка приложения которой описывает кривую L.

Криволинейный интеграл второго рода зависит от выбора направления обхода кривой; если изменить направление обхода, то интеграл меняет знак:

.

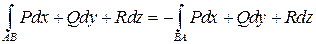Криволинейные интегралы первого и второго рода связаны формулой

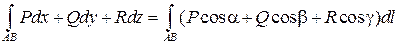, (7.17)

где a, b, g – углы между соответствующими осями координат и направлением касательной к линии АВ, отвечающим направлению интегрирования для интеграла в левой части равенства (7.17).

7.9 ВЫЧИСЛЕНИЕ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ

Вычисление криволинейного интеграла первого рода сводится к вычислению определенного интеграла.

Если пространственная кривая L задана параметрическими уравнениями х = x (t), у = y (t), z = z (t) (a £ t £ b), то

.

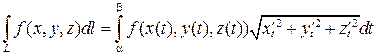Если кривая лежит в плоскости Oxy, то

.

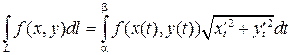В частности, для плоской кривой, заданной уравнением y = y (x) (a £ x £ b), имеем

.

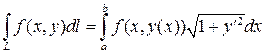Если плоская кривая задана уравнением r = r (j) (a £ j £ b) в полярных координатах, то

.

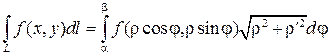Вычисление криволинейного интеграла второго рода также сводится к вычислению определенного интеграла.

Если кривая L задана параметрическими уравнениями х = x (t), у = y (t), z = z (t) (a £ t £ b) и значению a соответствует точка A, а значению b – точка B, то

.

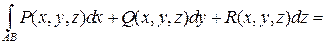
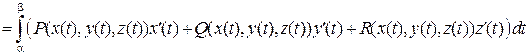В частности, для кривой L, лежащей в плоскости Oxy, получаем

.

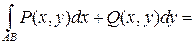
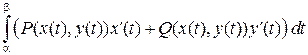Если плоская кривая L задана уравнением y = y (x) (a £ x £ b), то

.

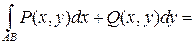
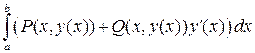7.10 ФОРМУЛА ГРИНА. УСЛОВИЯ НЕЗАВИСИМОСТИ
КРИВОЛИНЕЙНОГО ИНТЕГРАЛА ОТ ПУТИ ИНТЕГРИРОВАНИЯ

Если L – кусочно-гладкий контур, ограничивающий на плоскости Oxy область D, а P (x; y), Q (x; y) – функции непрерывные в замкнутой области D и имеющие в ней непрерывные частные производные, то справедлива формула Грина

,

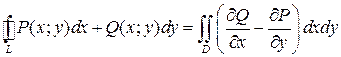где обход контура выбирается так, чтобы область D оставалась слева.

Криволинейный интеграл 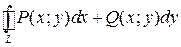, где контур L целиком лежит внутри некоторой односвязной области D, в которой функции P (x; y) и Q (x; y) непрерывны вместе со своими частными производными, не зависит от пути интегрирования тогда и только тогда, когда .

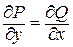В этом случае подынтегральное выражение представляет собой полный дифференциал некоторой функци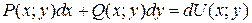и и

,

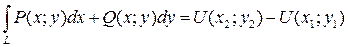где M ₁(x ₁; y ₁) и M ₂(x ₂; y ₂) – соответственно начальная и конечная точки пути интегрирования. В частности, криволинейный интеграл в этом случае по замкнутому контуру 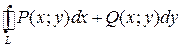= 0.

7.11 ПРИЛОЖЕНИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ

Длина l дуги AB плоской или пространственной кривой вычисляется по формуле

.

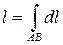В частности, если пространственная линия задана параметрическими уравнениями x = x (t), y = y (t), z = z (t) (a £ t £ b), то

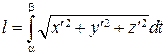. (7.18)

Площадь фигуры, расположенной в плоскости Oxy и ограниченной замкнутой линией L, находится по формуле

.

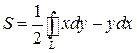Если 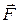= P (x; y; z) i + Q (x; y; z) j + R (x; y; z) k –переменная сила, совершающая работу A вдоль пути L, и функции P = P (x; y; z), Q = Q (x; y; z), R =R (x; y; z) непрерывны, то

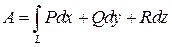. (7.19)

Если линия L лежит в плоскости Oxy, то формулы (7.18) и (7.19) упрощаются (так как соответствующие функции не зависят от z)

7.12 ИНТЕГРАЛЫ ПО ПОВЕРХНОСТИ

Интегралы первого рода. Пусть дана функция f (x; y; z), непрерывная на некоторой гладкой поверхности G. Разобьем поверхность G сеткой произвольно проведенных кривых на элементарные области D G ₁, D G ₂,…, D G_n. В каждой из областей D G_i выберем произвольно одну точку M_i (x_i; y_i; z_i), вычислим значение данной функции в этой точке и, умножив его на площадь соответствующей области поверхности, составим сумму всех таких произведений

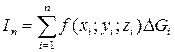, (7.20)

называемую интегральной суммой. Обозначим через d_i диаметр элементарной области поверхности D G_i, т.е. расстояние между наиболее удаленными ее точками; d – наибольший из указанных диаметров.

Интегралом первого рода от функции f (x, y, z) по поверхности G называется предел интегральной суммы (7.20) при d ® 0:

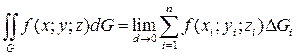. (7.21)

Интеграл первого рода по поверхности обладает свойствами, аналогичными свойствам криволинейных интегралов первого рода.

Если f (x, y, z) > 0 и функция f рассматривается как поверхностная плотность массы материальной поверхности G, то интеграл (7.21) определяет массу этой поверхности.

Интегралы второго рода. Пусть в точках двусторонней поверхности G задана непрерывная функция f (x; y; z). Выберем определенную сторону этой поверхности. Разобьем поверхность G сеткой произвольно проведенных кривых на элементарные области D G ₁, D G ₂,…, D G_n. В каждой области D G_i выберем произвольно одну точку M_i (x_i; y_i; z_i), вычислим в ней значение данной функции. Это значение f (x_i; y_i; z_i) умножим на площадь проекции D S_i области D G_i на плоскость Oxy (а не на площадь D G_i, как это было в случае интеграла первого рода). При этом числу D S_i приписывается определенный знак, а именно: если в точках области D G_i нормаль, отвечающая выбранной стороне поверхности, составляет с осью Oz острый угол, то через D S_i обозначаем площадь проекции D G_i, взятую со знаком «+», если же упомянутая нормаль составляет с осью Oz тупой угол, то под D S_i будем понимать площадь этой проекции, взятую со знаком «–». Составим сумму всех таких произведений:

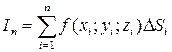. (7.22)

Интегралом второго рода от функции f (x; y; z) по поверхности G называется предел суммы (7.22) при d ® 0, где d – наибольший из диаметров элементарных областей D G_i:

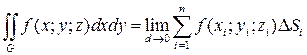. (7.23)

Аналогично определяются интегралы 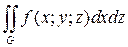, , 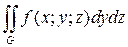причем для выбора знака проекции элемента служит угол между нормалью, отвечающей выбранной стороне, и осью Oy или Ox.

Наиболее общий вид интеграла второго рода:

,

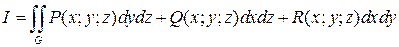где P, Q, R – функции от x, y, z, определенные и непрерывные в точках двусторонней поверхности G.

Интеграл второго рода обладает всеми свойствами интеграла первого рода, за исключением одного: при переходе к другой стороне поверхности интеграл (7.23) меняет знак.

Интегралы первого и второго рода связаны формулой

,

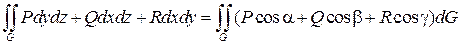где cos a, cos b, cos g – направляющие косинусы нормали, направленной в ту сторону поверхности, по которой берется интеграл второго рода.

Если поверхность G задана уравнением в неявном виде F (x; y; z) = 0, то направляющие косинусы нормали этой поверхности определяются по формулам:

, ,

,

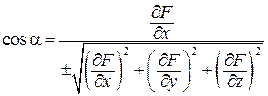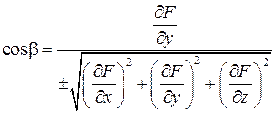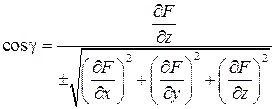где знак перед радикалом должен быть согласован со стороной поверхности.

7.13 ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ ПО ПОВЕРХНОСТИ

Предположим, что поверхность G однозначно проектируется на какую-либо координатную плоскость, например плоскость Oxy, и область S является ее проекцией, тогда элемент поверхности определяется формулой

,

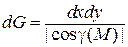где g(M) – угол между нормалью к поверхности в точке M (x; y; z) и осью Oz.

Если поверхность задана уравнением z = z (x; y), то ,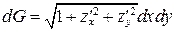

и интеграл 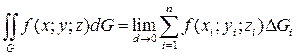вычисляется по формуле

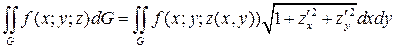. (7.24)

Интегралы второго рода вычисляются следующим образом. Если поверхность G однозначно проектируется в область S ₁ плоскости Oxy и z = f (x; y) – ее уравнение, то

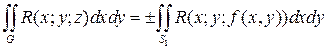, (7.25)

где знак «+» берется в том случае, когда на выбранной стороне поверхности cos g > 0, а знак «–» берется в случае, когда cos g < 0. Аналогично: если G однозначно проектируется в область S ₂ (или S ₃) на плоскость Oxz (или Oyz), т.е. может быть задана уравнением y = j(x; z) (или x = y(y; z)), то:

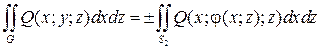, (7.26)

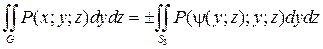, (7.27)

где в случае формулы (7.26) берется знак cos b, а в случае формулы (7.27) cos a.

Для вычисления интеграла общего вида используются те же формулы (7.25)–(7.27), если поверхность G однозначно проектируется на все три плоскости. В более сложных случаях поверхность G разбивается на части, обладающие указанными свойствами, а интеграл общего вида – на сумму интегралов по этим частям.

7.14 ФОРМУЛЫ СТОКСА И ОСТРОГРАДСКОГО-ГАУССА

Если функции P = P (x; y; z), Q = Q (x; y; z), R = R (x; y; z) непрерывны вместе со своими частными производными первого порядка, на поверхности G и L – замкнутый контур, ограничивающий поверхность G, то справедлива формула Стокса

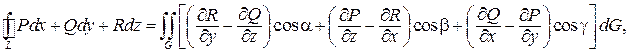
где cos a, cos b, cos g – направляющие косинусы нормали к поверхности G. Направление нормали определяется так, чтобы со стороны нормали обход контура L казался происходящим против хода часовой стрелки.

Если функции P = P (x; y; z), Q = Q (x; y; z), R = R (x; y; z) непрерывны вместе со своими частными производными первого порядка в замкнутой области D пространства, ограниченной замкнутой гладкой поверхностью G, то справедлива формула Остроградского-Гаусса

,

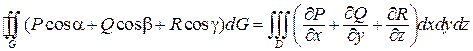где cos a, cos b, cos g – направляющие косинусы внешней нормали к поверхности G.

7.15 ПРИЛОЖЕНИЯ ИНТЕГРАЛОВ ПО ПОВЕРХНОСТИ

Площадь S_G поверхности G вычисляется по формуле

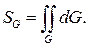
Если g = g(x, y, z) – поверхностная плотность массы материальной поверхности G, то масса этой поверхности определяется интегралом

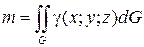. (7.28)

Координаты центра тяжести C_o (x_o; y_o; z_o) поверхности G вычисляются по формулам:

, , ,

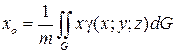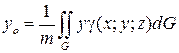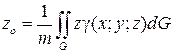где m определяется формулой (7.28).

7.16 СКАЛЯРНОЕ ПОЛЕ

Скалярное поле определяется скалярной функцией u = u (M) = u (x; y; z) = u (r), где M (x; y; z) – точка пространства; r = x i + y j + z k – радиус-вектор точки M. Другими словами, если каждой точке M области D поставлена в соответствие скалярная величина, то говорят, что в области D задано скалярное поле.

Если существует декартова система координат, в которой функция u не зависит от одной из координат, например z, т.е. u = u (x; y), то скалярное поле называется плоским. Такое поле принимает одинаковые значения на каждой прямой, параллельной оси Oz, поэтому его обычно рассматривают только в плоскости Oxy.

Поверхностями уровня скалярного поля u = u (x; y; z) называются поверхности, определяемые уравнением u (x; y; z) = С, где C – произвольная постоянная.

Градиентом скалярного поля, определяемого непрерывной дифференцируемой функцией u = u (x; y; z), называется вектор

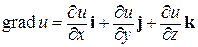. (7.29)

Градиент поля u в данной точке M (x; y; z) направлен по нормали к поверхности уровня u (x, y, z) = С, проходящей через точку M. Величина этого вектора для каждой точки поля определяется формулой

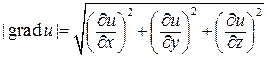. (7.30)

В направлении градиента скорость изменения функции и будет наибольшей.

Градиент скалярного поля обозначается символом Ñ u (знак Ñ читается «набла»). Таким образом,

.

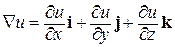Отметим, что Ñ можно рассматривать как дифференциальный оператор (оператор Гамильтона)

,

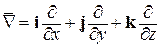который, будучи применен к скаляру u, дает grad u. Этот оператор удобно рассматривать как символьный вектор и применять к нему обычные правила векторной алгебры. Например, скалярное произведение

.

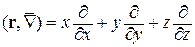Производная скалярного поля u = u (x; y; z) по направлению l, заданному вектором a = a_x i + a_y j + a_z k, вычисляется по формуле

,

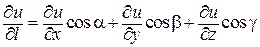где

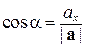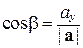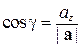; ; ; | a | = .

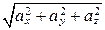Производная по направлению и градиент скалярного поля u (M) в данной точке M связаны формулой

,

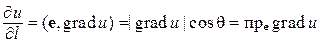где e – единичный вектор заданного направления l; q – угол между градиентом и вектором e в точке M.

Точка, в которой производная скалярного поля по любому направлению равна нулю, называется стационарной.

7.17 ВЕКТОРНОЕ ПОЛЕ

Векторное поле определяется векторной функцией

,

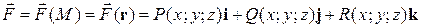где M (x; y; z) – точка пространства; r = x i + y j + z k – радиус-вектор точки M. Другими словами, если каждой точке M области D поставлена в соответствие векторная величина, то говорят, что в области D задано векторное поле.

Векторной линией называется кривая, направление которой в каждой ее точке M совпадает с направлением вектора 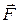, соответствующего этой точке. Векторная линия определяется системой дифференциальных уравнений

.

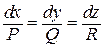Дивергенцией векторного поля 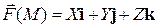называется скаляр

.

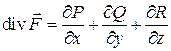Вихрем (ротором) векторного поля 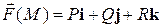называется вектор

.

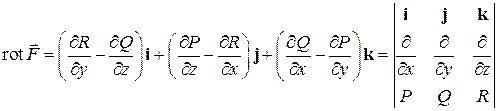Потоком векторного поля 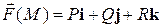через поверхность G в сторону, определяемую единичным вектором нормали 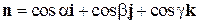к поверхности G, называется поверхностный интеграл

,

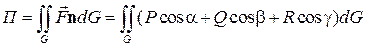где 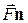– скалярное произведение вектора 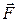и 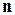единичного вектора выбранного направления нормали.

Линейным интегралом от вектора 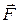по ориентированной кривой K называется криволинейный интеграл

,

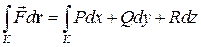представляющий собой работу векторного поля вдоль кривой K. Если контур C замкнутый, то линейный интеграл

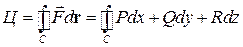
называется циркуляцией векторного поля 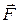вдоль контура C.

Формула Остроградского-Гаусса в векторной форме имеет вид

,

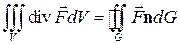т.е. интеграл от дивергенции векторного поля 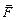, распространенный по некоторому объему V, равен потоку вектора через поверхность G, ограничивающую данный объем.

Формула Стокса в векторной форме имеет вид

,

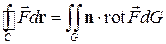т.е. циркуляция вектора вдоль замкнутого контура С, ограничивающего некоторую поверхность G, равна потоку вихря через эту поверхность (направление обхода контура и нормали должны быть согласованы друг с другом).

Векторное поле 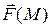называется безвихревым, если rot 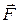= 0.

Векторное поле 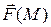называется потенциальным, если 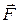= grad u, т.е. если , , 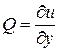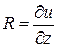. В этом случае rot 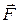= rot (grad u) = Ñ´Ñ u = 0. Следовательно, потенциальное поле является безвихревым.

Потенциал векторного поля может быть найден по формуле

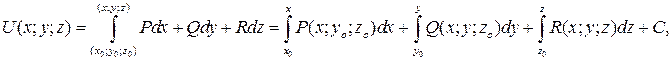
где (x _o; y _o; z _o) – координаты фиксированной точки, (x; y; z) – координаты произвольной точки. Потенциал определяется с точностью до произвольного постоянного слагаемого (из-за того, что grad (U + C) = grad U).

Векторное поле 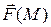называется соленоидальным (или трубчатым), если div 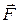= 0, т.е. в области задания поля V отсутствуют и стоки, и источники. Так как

div (rot 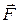) = Ñ(Ñ´ 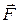) = 0, то поле вихрей является соленоидальным.

КОНТРОЛЬНЫЕ ВОПРОСЫ

Двойной интеграл. Его вычисление сведением к повторному интегрированию. Замена переменной в двойном интеграле. Переход к полярным координатам. Решение задач механики с помощью двойных интегралов.

Тройной интеграл. Вычисление в декартовых, цилиндрических и сферических координатах.

Задачи, приводящие к криволинейным интегралам. Вычисление криволинейного интеграла. Формула Грина. Нахождение функции по её полному дифференциалу. Площадь поверхности. Определение поверхностных интегралов, основные свойства и вычисление. Скалярное поле. Производная по направлению. Градиент.

Односторонние и двусторонние поверхности. Поток векторного поля через поверхность и его физический смысл. Теорема Остроградского – Гаусса. Дивергенция векторного поля. Циркуляция поля. Теорема Стокса. Ротор векторного поля. Соленоидальные и потенциальные поля. Оператор Гамильтона.