2015-09-06
569
Загальне рішення неоднорідного лінійного рівняння - сума його частинного рішення і загального рішення відповідного однорідного рівняння. Метод варіації довільних сталих працює, якщо відома фундаментальна система розв'язків лінійного рівняння. Основну ідею викладемо для найпростішого випадку неоднорідного рівняння другого порядку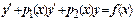 
(1 )
Нехай y 1(x), y 2(x) - фундаментальна система рішеньвідповідногооднорідногорівняння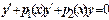 
,(2)
y (x) = C 1 y 1(x) + C 2 y 2(x) - загальнерішенняоднорідногорівняння (2). Ідея методу варіаціїдовільнихсталихполягає в наступному. Шукаємозагальнерішеннянеоднорідногорівняння (1) в тому ж вигляді y (x)= C 1(x) y 1(x) + C 2(x) y 2(x), припускаючи, щопостійні C1, C2 - не постійні, а функції, щозалежатьвід x: C 1 = C 1 (x), C 2 = C 2(x). Знаходимопохідну. Далі треба обчислювати другу похідну.Скористаємосятієюобставиною, щозамістьоднієїфункції y (x) ми шукаємодвіфункції C1 (x) і C2 (x), і, як наслідок, можемонакластидовільнийзв'язок на ціфункції. Для того, щоб у виразі для другоїпохідної не брали участь другіпохідніфункцій C1 (x) і C2 (x), в якостіцьомузв'язкупокладемо: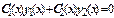 
(3 )
|
|
|
Тоді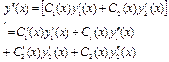 
Підставляємовирази для y (x) та їїпохідних в рівняння(1):
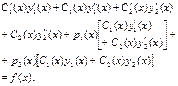
Перетворимо:
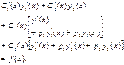
Вирази в квадратних дужках дорівнюють нулю, так як функції y1 (x), y2 (x) - рішенняоднорідногорівняння (2), тому остаточно
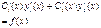(4)
Рівняння (3),(4) даютьзамкнену систему для функцій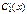 
и 
:
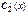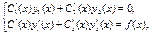(5)
визначникцієїсистемизбігається з вронскіаномфункцій y1 (x), y2 (x) і тому відміннийвід нуля, отже, система маєєдинерішення,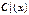 
, 
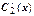. Знаходячицерішення і інтегруючивиразипохідних для і, отримаємо 
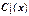и 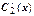, получим C 1 (x) и C 2(x), а значить, і загальнерішеннянеоднорідногорівняння (1) y (x) = C 1 y 1(x) + C 2 y 2(x).
