Вычисление интегралов по формулам прямоугольников, трапеций и формуле Симпсона. Оценка погрешностей.
Методические указания по теме 4.1:
Вычисление интегралов по формулам прямоугольников. Оценка погрешности:
Решение многих технических задач сводится к вычислению определенных интегралов, точное выражение которых сложно, требует длительных вычислений и не всегда оправдано практически. Здесь бывает вполне достаточно их приближенного значения. Например, необходимо вычислить площадь, ограниченную линией, уравнение которой неизвестно, осью х и двумя ординатами. В этом случае можно заменить данную линию более простой, для которой известно уравнение. Площадь полученной таким образом криволинейной трапеции принимается за приближенное значение искомого интеграла. Геометрически идея способа вычислений определенного интеграла по формуле прямоугольников состоит в том, что площадь криволинейной трапеции А1АВВ1 заменяется площадью равновеликого прямоугольника А1А2В1В2, которая по теореме о среднем равна
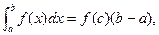 где f(c) --- высота прямоугольника А1А2В1В2 , представляющая собой значение подынтегральной функции в некоторой промежуточной точке c(a< c<b).
где f(c) --- высота прямоугольника А1А2В1В2 , представляющая собой значение подынтегральной функции в некоторой промежуточной точке c(a< c<b).
Практически трудно найти такое значение с, при котором (b-a) f (c) в точности равнялось бы 
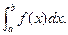 . Для получения более точного значения площадь криволинейной трапеции разбивают на n прямоугольников, высоты которых равны y0, y1, y2, …,y n-1 и основания
. Для получения более точного значения площадь криволинейной трапеции разбивают на n прямоугольников, высоты которых равны y0, y1, y2, …,y n-1 и основания 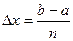 .
.
Если суммировать площади прямоугольников, которые покрывают площадь криволинейной трапеции с недостатком, функция 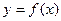 --- неубывающая, то вместо формулы используют формулу
--- неубывающая, то вместо формулы используют формулу
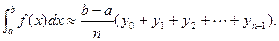
Если с избытком, то
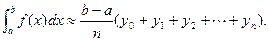
Значения 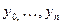 находят из равенств
находят из равенств 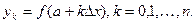 . Эти формулы называются формулами прямоугольников и дают приближенный результат. С увеличением n результат становится более точным.
. Эти формулы называются формулами прямоугольников и дают приближенный результат. С увеличением n результат становится более точным.
Пример 1. Вычислить по формуле прямоугольников 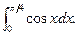
Разделим промежуток интегрирования на 5 частей. Тогда 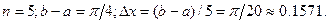 . При помощи калькулятора или таблицы найдем значения подынтегральной функции (с точностью до 4-х знаков после запятой):
. При помощи калькулятора или таблицы найдем значения подынтегральной функции (с точностью до 4-х знаков после запятой):
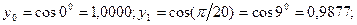
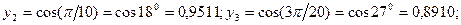
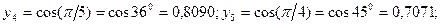
По формуле прямоугольников (с недостатком)
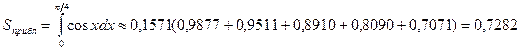
С другой стороны по формуле Ньютона-Лейбница
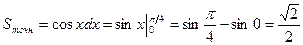
Найдем относительную погрешность вычисления по формуле прямоугольников:
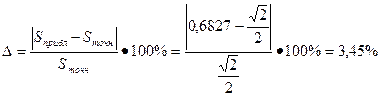
Вычисление интегралов по формулам трапеций. Оценка погрешности:
Геометрический смысл следующего способа приближенного вычисления интегралов состоит в том, что нахождение площади приблизительно равновеликой «прямолинейной» трапеции.
Пусть необходимо вычислить площадь А1АmBB1 криволинейной трапеции, выражаемую формулой 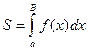 .
.
Заменим дугу AmB хордой AB и вместо площади криволинейной трапеции А1АmBB1 вычислим площадь трапеции А1АBB1: 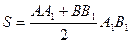 , где AA1 и ВВ 1-- основания трапеции, а A1 В 1 –ее высота.
, где AA1 и ВВ 1-- основания трапеции, а A1 В 1 –ее высота.
Обозначим f(a)=A1A,f(b)=B1B. высота трапеции A1B1=b-a, площадь 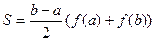 . Следовательно,
. Следовательно, 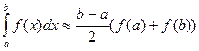 или
или
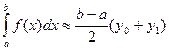
Это так называемая малая формула трапеций.
Для получения более точного результата необходимо разбить площадь криволинейной трапеции на n площадей ординатами, отстоящими друг от друга на расстоянии 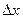 . Суммируем площади получившихся трапеций:
. Суммируем площади получившихся трапеций: 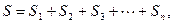
где по малой формуле трапеций
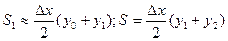
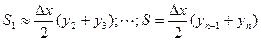
Сложив, получим
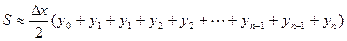 ,
,
или
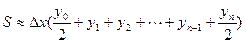 ,
,
так как 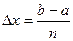 и
и 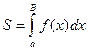 , то можно записать так называемую большую формулу трапеций:
, то можно записать так называемую большую формулу трапеций: 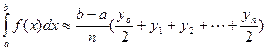 , где y0,y1,y2,..,.yn --- значения подынтегральной функции при значениях аргумента, соответственно,
, где y0,y1,y2,..,.yn --- значения подынтегральной функции при значениях аргумента, соответственно, 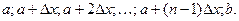
Пример 2. Ширина реки 26 м, промеры глубины в поперечном сечении реки через каждые 2 м дали, следующие результаты:
| х | ||||||||||||||
| у | 0,3 | 0,9 | 1,7 | 2,1 | 2,8 | 3,4 | 3,3 | 3,0 | 3,5 | 2,9 | 1,7 | 1,2 | 0,8 | 0,6 |
х —расстояние от одного берега, а у --- соответствующая глубина в метрах.
Зная, что средняя скорость течения 1,3 м/с, определить секундный расход Q воды в реке.
По формуле трапеций площадь поперечного сечения
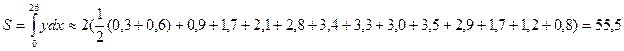 Секундный расчет воды Q получим, если умножим эту площадь поперечного сечения на скорость течения реки:
Секундный расчет воды Q получим, если умножим эту площадь поперечного сечения на скорость течения реки: 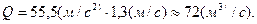
Здесь точно оценить погрешность нельзя. Некоторые косвенные методы оценок позволяют указать приближенно, что погрешность вычисления площади S составляет примерно 3м2, значит, погрешность вычисления Q составляет примерно 4 м3/с.
Пример 3. По формуле трапеций вычислить 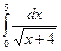 при n=5.
при n=5.
Положим 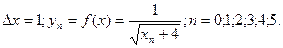
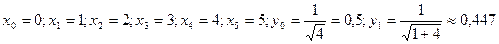 ,
,
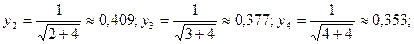
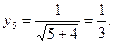
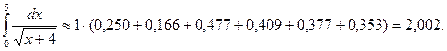
Вычисление интегралов по формуле Симпсона:
Это более совершенный способ – график подынтегральной функции приближается не ломаной линией, а маленькими параболами. Сколько промежуточных отрезков – столько и маленьких парабол. Если взять те же три отрезка, то метод Симпсона даст ещё более точное приближение, чем метод прямоугольников или метод трапеций. Задача на вычисление определенного интеграла по формуле Симпсона – самая популярное задание на практике. И методу парабол будет уделено значительное внимание.
Рассмотрим определенный интеграл 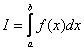 , где
, где 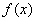 – функция, непрерывная на отрезке
– функция, непрерывная на отрезке 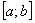 . Проведём разбиение отрезка
. Проведём разбиение отрезка 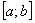 на чётное количество равных отрезков. Чётное количество отрезков обозначают через
на чётное количество равных отрезков. Чётное количество отрезков обозначают через 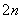 .
.
Итак, наше разбиение имеет следующий вид:
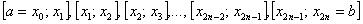
Термины аналогичны терминам метода трапеций:
Точки 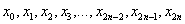 называют узлами.
называют узлами.
Формула Симпсона для приближенного вычисления определенного интеграла имеет следующий вид:
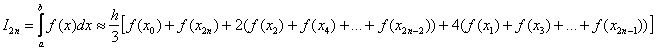 где:
где:
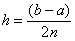 – длина каждого из маленьких отрезков или шаг;
– длина каждого из маленьких отрезков или шаг;
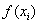 – значения подынтегральной функции в точках
– значения подынтегральной функции в точках 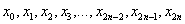 .
.
Детализируя это нагромождение, разберу формулу подробнее:
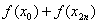 – сумма первого и последнего значения подынтегральной функции;
– сумма первого и последнего значения подынтегральной функции;
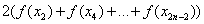 – сумма членов с чётными индексами умножается на 2;
– сумма членов с чётными индексами умножается на 2;
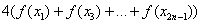 – сумма членов с нечётными индексами умножается на 4.
– сумма членов с нечётными индексами умножается на 4.
Пример 4.Вычислить приближенно определенный интеграл по формуле Симпсона с точностью до 0,001. Разбиение начать с двух отрезков 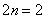
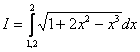
Необходимо вычислить определенный интеграл с определенной точностью.. Как и для метода трапеций, существует формула, которая сразу позволит определить нужное количество отрезков, чтобы гарантированно достичь требуемой точности. Если у нас два отрезка разбиения 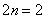 , то узлов будет на один больше:
, то узлов будет на один больше: 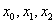 . И формула Симпсона принимает весьма компактный вид:
. И формула Симпсона принимает весьма компактный вид:
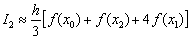
Вычислим шаг разбиения: 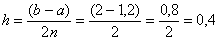
Заполним расчетную таблицу:
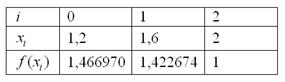
Еще раз комментирую, как заполняется таблица:
В верхнюю строку записываем «счётчик» индексов
Во второй строке сначала пишем нижний предел интегрирования 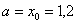 , а затем последовательно приплюсовываем шаг
, а затем последовательно приплюсовываем шаг 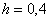 .
.
В третью строку заносим значения подынтегральной функции. Например, если 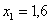 , то
, то 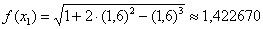 . В результате:
. В результате:
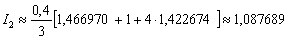
Первичный результат получен. Теперь удваиваем количество отрезков до четырёх: 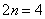 . Формула Симпсона для данного разбиения принимает следующий вид:
. Формула Симпсона для данного разбиения принимает следующий вид:
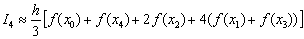
Вычислим шаг разбиения: 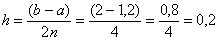
Заполним расчетную таблицу:

Таким образом:
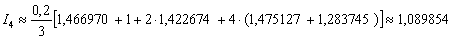
Оцениваем погрешность:
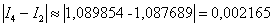
Погрешность больше требуемой точности: 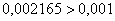 , поэтому необходимо еще раз удвоить количество отрезков:
, поэтому необходимо еще раз удвоить количество отрезков: 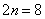 .
.
Формула Симпсона примет вид:
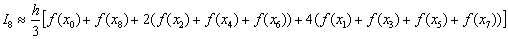
Вычислим шаг: 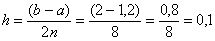
И снова заполним расчетную таблицу:

Таким образом:
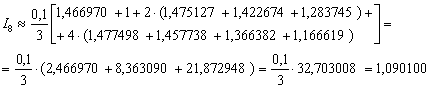
Оцениваем погрешность:
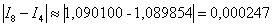
Погрешность меньше требуемой точности: 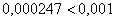 . Осталось взять наиболее точное приближение
. Осталось взять наиболее точное приближение 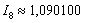 , округлить его до трёх знаков после запятой и записать:
, округлить его до трёх знаков после запятой и записать:
Ответ: 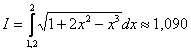 с точностью до 0,001
с точностью до 0,001
Вопросы для самопроверки по теме 4.1:
1.Какой вид имеет формула прямоугольников?
2.Какой вид имеет формула трапеций?
3.Какой вид имеет формула Симпсона?
Задания для самостоятельного решения по теме 4.1:
1. Вычислите по формуле прямоугольников:
a) 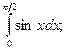 б)
б) 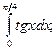 .
.
2. Вычислите по формуле трапеций 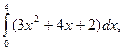 , разбивая отрезок на 4 равные части; найдите его точное значение по формуле Ньютона-Лейбница и относительную погрешность
, разбивая отрезок на 4 равные части; найдите его точное значение по формуле Ньютона-Лейбница и относительную погрешность 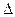 в процентах.
в процентах.
3. Вычислите по формуле трапеций 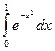 с точностью до 0,001.
с точностью до 0,001.
4. По формуле трапеций вычислите, 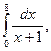 приняв n=8.
приняв n=8.
5.Вычислить приближенно определенный интеграл по формуле Симпсона с точностью до 0,0001. Разбиение начать с двух отрезков 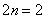
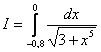 .
.
 2015-10-16
2015-10-16 10072
10072








