Нахождение значения функции с использованием метода Эйлера. Численное решение обыкновенных дифференциальных уравнений.
Методические указания по теме 4.3:
Нахождение значения функции с использованием метода Эйлера. Численное решение обыкновенных дифференциальных уравнений:
Уравнения, содержащие производную функции одной переменной, возникают во многих областях прикладной математики. Вообще говоря, любая физическая ситуация, где рассматривается степень изменения одной переменной по отношению к другой переменной, описывается дифференциальным уравнением, а такие ситуации встречаются довольно часто. Решение обыкновенных дифференциальных уравнений (нелинейных) первого порядка с начальными данными (задача Коши) - классическая область применения численных методов. Используется метод Эйлера, один из самых старых и широко известных методов численного интегрирования дифференциальных уравнений. Этот метод имеет довольно большую ошибку; кроме того, он очень часто оказывается неустойчивым - малая начальная ошибка быстро увеличивается с ростом Х. Поэтому чаще используют более точные методы, такие как: исправленный метод Эйлера и модифицированный метод Эйлера. Метод Эйлера относиться к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Решить дифференциальное уравнение у/=f (x, y) численным методом - это значит для заданной последовательности аргументов х0, х1…, хn и числа у0, не определяя функцию у=F(x), найти такие значения у1, у2,…, уn, что уi=F(xi) (i=1,2,…, n) и F(x0)=y0.
Таким образом, численные методы позволяют вместо нахождения функции У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=xk-xk-1 называется шагом интегрирования.
Метод Эйлера относится к численным методам, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.
Пример 1.Найти решение уравнения y/=f (x, y) с начальным условием x=x0, y(x0)=y0 на отрезке [а, b].
Разобьем отрезок [a, b] на n равных частей и получим последовательность х0, х1, х2,…, хn, где xi=x0+ih (i=0,1,…, n), а h=(b-a)/n-шаг интегрирования.
В методе Эйлера приближенные значения у(хi)yi вычисляются последовательно по формулам уi+hf(xi, yi) (i=0,1,2…).
Если правая часть уравнения в некотором прямоугольнике R {|x-x0|a, |y-y0|b} удовлетворяет условиям:
|f (x, y1) - f (x, y2)| N|y1-y2| (N=const), |df/dx|=|df/dx+f (df/dy)| M (M=const), то имеет место следующая оценка погрешности: |y(xn) - yn| hM/2N[(1+hN)n-1], где у(хn) - значение точного решения уравнения(1) при х=хn, а уn - приближенное значение, полученное на n-ом шаге.
Формула имеет в основном теоретическое применение. На практике иногда оказывается более удобным двойной просчет: сначала расчет ведется с шагом h, затем шаг дробят и повторный расчет ведется с шагомh/2. Погрешность более точного значения уn* оценивается формулой |yn-y(xn)||yn*-yn|.
В исправленном методе Эйлера находят средний тангенс наклона касательной для двух точек: xm, ym и xm+h, ym+hy'm. Последняя точка есть та самая, которая в простом методе обозначалась xm+1, ym+1. Геометрический процесс нахождения точки xm+1, ym+1 можно проследить по рисунку 2. С помощью метода Эйлера находится точка xm+h, ym+hy'm, лежащая на прямой L1. В этой точке снова вычисляется тангенс угла наклона касательной, на рисунке этому значению соответствует прямая L2. Усреднение двух тангенсов дает прямую L'3. Наконец, через точку xm, ym мы проводим прямую L3 параллельную L'3. Точка, в которой прямая L3 пересечется с ординатой, восстановленной из x= xm+1=xm+h, и будет искомой точкой y= ym+1= ym+hy'm. Тангенс угла наклона L3 равен:
F(xm, ym)=1/2 [f(xm, ym)+f(xm+h, ym+hy'm)], где ym = f(xm, ym)
Уравнение линии L3 при этом записывается в виде: y = ym + (x - xm)*F(xm)
так что:
ym+1 = ym + h*F(xm) (8)
Модифицированный метод Эйлера более точен. Рассмотрим дифференциальное уравнение у/=f (x, y) с начальным условием y(x0)=y0. Разобьем наш участок интегрирования на n равных частей. На малом участке [x0, x0+h] интегральную кривую заменим прямой линией. Получаем точку Мк(хк, ук). Через Мк проводим касательную: y=yк=f(xk, yk) (x-xk). Делим отрезок (xк, xк1) пополам: xh+k/=xk+h/2=xk+1/2 ,
yh+k/=yk+f(xk, yk) h/2=yk+yk+1/2
Получаем точку Nk/. В этой точке строим следующую касательную:
y(xk+1/2)=f(xk+1/2, yk+1/2)=бk (11)
Из точки Мк проводим прямую с угловым коэффициентом бк и определяем точку пересечения этой прямой с прямой xк1. Получаем точку Мк/. В качестве ук+1 принимаем ординату точки Мк/. Тогда:yк+1=yк+бкh, xk+1=xk+h,бk=f(xk+h/2, xk+f(xk, yk) h/2),
yk=yk-1+f(xk-1, yk-1) h.
Эти формулы называются рекуррентными формулами метода Эйлера.
Сначала вычисляют вспомогательные значения искомой функции yк+1/2 в точках xк+1/2, затем находят значение правой части уравнения в средней точке y/k+1/2=f(xk+1/2, yk+1/2) и определяют yк+1.
Метод Эйлера являлся исторически первым методом численного решения задачи Коши. О. Коши использовал этот метод для доказательства существования решения задачи Коши. Ввиду невысокой точности и вычислительной неустойчивости для практического нахождения решений задачи Коши метод Эйлера применяется редко. Однако в виду своей простоты метод Эйлера находит свое применение в теоретических исследованиях дифференциальных уравнений, задач вариационного исчисления и ряда других математических проблем.
Основные правила дифференцирования:
Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.
1) (u ± v)¢ = u¢ ± v¢
2) (u×v)¢ = u×v¢ + u¢×v
3) 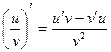 , если v ¹ 0
, если v ¹ 0
Производные основных элементарных функций.
1)С¢ = 0; 9) 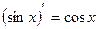
2)(xm)¢ = mxm-1; 10) 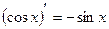
3) 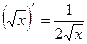 11)
11) 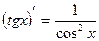
4) 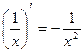 12)
12) 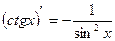
5) 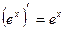 13)
13) 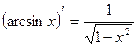
6) 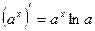 14)
14) 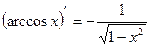
7) 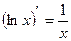 15)
15) 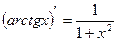
8) 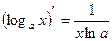 16)
16) 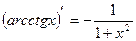
17) (lnïxï)¢= 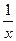 ,
,
Свойства неопределенного интеграла:
1. 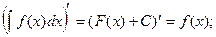
2. 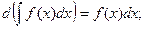
3. 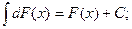
4. 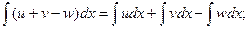 где u, v, w – некоторые функции от х.
где u, v, w – некоторые функции от х.
5. 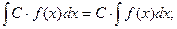
«Табличные» интегралы:
| Интеграл | Значение | |
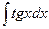 | -ln½cosx½+C | |
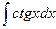 | ln½sinx½+ C | |
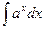 | 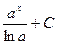 | |
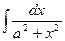 | 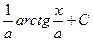 | |
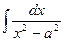 | 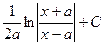 | |
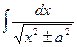 | ln 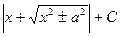 | |
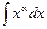 | 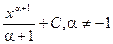 | |
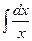 | 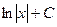 | |
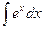 | ex + C | |
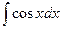 | sinx + C | |
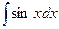 | -cosx + C | |
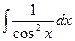 | tgx + C | |
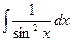 | -ctgx + C | |
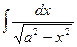 | arcsin 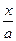 + C + C | |
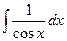 | 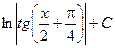 | |
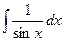 | 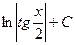 |
Вопросы для самопроверки по теме 4.3:
1.Сформулируйте метод Эйлера.
2.Напишите формулы «табличных» интегралов.
3.Сформулируйте свойства неопределенного интеграла.
Задания для самостоятельного решения по теме 4.3:
1.Вычислите интеграл:
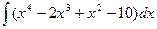 | 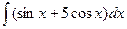 |
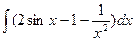 | 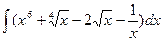 |
| 2.Решите уравнение: | |
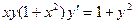 . . |
 2015-10-16
2015-10-16 2414
2414
