Средней арифметической вариационного ряда называется дробь, числитель которой- сумма произведений вариант ряда, а знаменатель- объем выборки или соответствующие им веса.
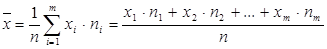
Пример: Вычислить среднее число обрывов нити на станке за время t.
| Кол-во обрывов | Кол-во промежутков | 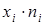 |
| Итого: 36 |
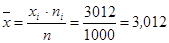
Теорема: Если варианты увеличить или уменьшить в одно и тоже число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз.
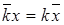 ;
;
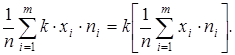
Пример 2.
Приведено распределение по заработной плате. Вычислить среднюю з/п рабочих цеха №1.
| З/плата, руб. | Число рабочих цеха | Всего | ||
| цех№1 | цех№2 | цех№3 | ||
| 70-80 80-90 90-100 100-110 110-120 120-130 | - - | - - | ||
| Итого: |
| Средняя з/плата | Цех№1 | 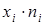 |
| - - | - - | |
| Итого: |
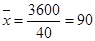
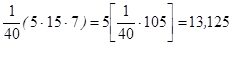
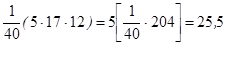
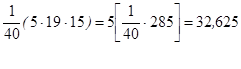
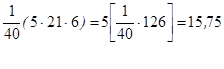
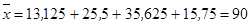 ;
;
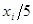 | ni | 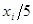 ni ni |
| Итого: |
Теорема №2: Если варианты уменьшить или увеличить на одно и тоже число раз, то средняя арифметическая уменьшится на то же число раз.
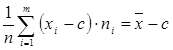 ;
;
Пример: Вычислить среднюю з/плату рабочих цеха№2,применяя теорему №2.
| xi | xi-c | Ni | 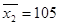 |
| -30 -20 -10 | -30 -100 -90 |
c - берем равное 105, что соответствует варианту с наибольшей частотой.
Теорема №3.
Сумма произведений отклонений вариантов от средней арифметической на соответствующие веса равна 0.
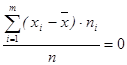 .
.
Теорема №4.
При увеличении или уменьшении весов в одно и тоже число раз, средняя арифметическая не меняется.
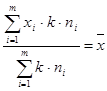 ;
;
Используя эту теорему, вычислим среднюю з/п цеха №3.
| З/плата | цех№3 | ni/4 | ni/4×k |
| - - | - - | - - | |
| Итого: |
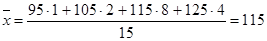 ; k =4.
; k =4.
Пусть некоторая совокупность разбита на группы не обязательно одинаковые по объему, тогда среднюю арифметическую распределения членов группы называют групповыми средними, а средние арифметические распределения по тому же признаку всей совокупности - общей средней. Группы называются непересекающимися, если каждый член совокупности принадлежит только одной группе.
Пусть распределение признака s в s - непересекающихся группах S 1, S 2,… S n и по всей совокупности s представлены в таблице:
| xi | S1 | S2 | ….. | Sl | S |
| x 1 | P 1 | q 1 | ….. | r 1 | P 1+ q 1+…+ r 1= n 1 |
| x 2 | P 2 | q 2 | ….. | r 2 | P 2+ q 2+…+ r 2= n 2 |
| ….. | ….. | ….. | ….. | ….. | ….. |
| x m | P m | q m | ….. | rm | Pm + qm +…+ rm = nm |
| Итого: | N 1 | N 2 | ….. | Nml | 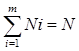 |
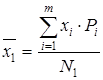 ;
; 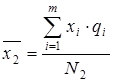 ;
; 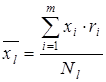 ;
; 
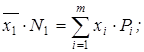
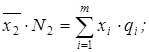
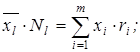
Общая средняя того же признака 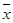 :
:
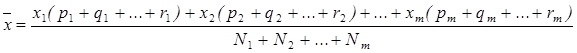 ;
;
Сгруппируем
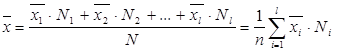 ;
;
Теорема №5
Общая средняя равна средней арифметической групповых средних всех непересекающихся групп.
Пример: Вычислить среднюю з/плату рабочих всего предприятия.
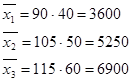 ;
;
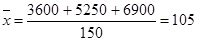 ;
;
Теорема №6
Если каждое значение признака z представляет сумму или разность значений x и y, то средняя арифметическая признака z равна сумме или разности средних арифметических x и y.
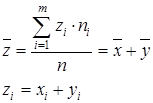 ;
;
 2015-10-16
2015-10-16 7748
7748
