9.1. Физическая (психологическая)
имитация деятельности оператора
Широкое место в арсенале методов инженерной психологии занимают имитационные методы. Выделение их в отдельную группу является несколько условным, поскольку их в ряде случаев трудно отделить от психологических или математических методов. В то же время, как указывалось в главе V, этим методам присущи специфические особенности, что и позволяет, хотя бы и условно, выделить имитационные методы в особую группу.
В самом общем плане имитация (от лат. imitatio — подражание, подделка) может быть определена как воспроизведение характеристик некоторой системы, ситуации, события или явления в обстановке, отличной от той, в которой протекает реальная деятельность оператора [105]. Средства, с помощью которых может быть достигнуто это воспроизведение, могут быть физическими или символическими (в частности, цифровыми). Физическая имитация может быть такой точной, что ее бывает трудно отличить от оригинала, который она имитирует. Примером этого могут быть различного рода военные учения. Символическая имитация может быть достаточно полной копией протекающих в оригинале процессов, но наглядного сходства с ним в этом случае обычно не бывает. Примером этого является моделирование реальных процессов методом статистических испытаний (метод Монте-Карло).
Имитация деятельности оператора (группы операторов) может быть частичной или полной. Физическая имитация, как правило, имеет частичный характер, поскольку, хотя физические характеристики процесса или системы можно воспроизвести достаточно полно, оперативные условия деятельности не поддаются такому полному воспроизведению. При полной имитации характеристики системы, окружающей среды вместе с их входными сигналами и ответными реакциями представлены символически, посредством математических выражений. Все операции этой математической системы выполняются вычислительной машиной с помощью метода статистических испытаний [105]. При этом различают аналитическое имитационное моделирование и статистическое имитационное моделирование [137]. Их особенности и основные отличия будут рассмотрены ниже.
Помимо рассмотренного, А.И. Нафтульев предлагает различать динамическую и цифровую имитацию. Первая протекает в реальном, вторая — в ускоренном масштабе времени. Основное отличие динамической имитации от цифровой заключается в основном в том, что в первом случае человек как бы непосредственно выполняет (имитирует) свои функции, а во втором — основные его функции имитируются с помощью ЭВМ. Подытоживая все сказанное следует отметить, что физическая имитация обычно носит частичный характер и осуществляется в реальном масштабе времени; символическая имитация, напротив, может носить более полный характер и протекает в ускоренном масштабе времени.
Важнейшей формой физической имитации является деловая игра. Она представляет метод имитации управленческих и деловых ситуаций путем игры по заданным правилам человека (группы людей) и ЭВМ. Деловая игра является формой воссоздания предметного и социального содержания профессиональной деятельности, моделирования систем отношений, характерных для данного вида практики. Проведение деловой игры представляет собой развертывание особой (игровой) деятельности участников на имитационной модели, воссоздающей условия и динамику производства. В зависимости от того, какой тип человеческой практики воссоздается в игре и каковы цели участииков, различают деловые игры учебные, исследовательские, управленческие, аттестационные. Деловые игры получили широкое распространение в связи с задачами по совершенствованию управления, принятия плановых и производственных решений, подготовки и повышения квалификации кадров. Учебная деловая игра позволяет задать в обучении предметный и социальный контексты будущей профессиональной деятельности и тем самым смоделировать более адекватные по сравнению с традиционным обучением условия формирования личности специалиста. В этих условиях усвоение нового знания накладывается на канву будущей профессиональной деятельности; обучение приобретает совместный, коллективный характер; формирование специалиста осуществляется в результате подчинения двум типам норм: нормам компетентных предметных действий и нормам отношений в групповой деятельности. Мотивация, интерес и эмоциональный статус участников деловой игры обусловливаются широкими возможностями для целеполагания и целеосуществления, диалогического общения на материале проблемно представленного содержания деловой игры. В инженерной психологии деловые игры широко применяются для подготовки операторов энергосистем, в психологии управления — для подготовки различного рода управленческих кадров.
Рассмотрим более подробно на конкретных примерах возможные случаи применения деловых игр для решения указанных задач.
В работе [197] обоснована необходимость формирования оперативных навыков и умений — заключительного этапа подготовки операторов энергоблоков — посредством деловых (оперативных) игр. Для этого в оперативной деятельности персонала энергоблоков было выделено игровое начало, найден подлинный соревновательный элемент. Например, обучаемому поручалась роль энергоблока, и он должен был правильно реагировать на управляющие действия другого обучаемого. Или один из игроков «изобретает аварию», а другой игрок — устраняет отказы. Помимо этого разработаны сценарии для проведения оперативных игр при возникновении тех или иных ситуаций в технологическом процессе.
Это позволило создать не просто игровую обучающую систему, но прежде всего — игровую тренирующую систему. Данный аспект является принципиально важным, так как позволяет ликвидировать разрыв между знаниями и умениями, между обучением и тренировкой. Тренирующее качество именно и достигнуто посредством оперативных игр. Для решения этих задач разработано несколько разновидностей таких игр: ситуационные (наблюдение, диагностика, планирование), координационные (взаимодействие с автоматикой), противоаварийные.
Рассмотрение особенностей проведения таких игр обсудим для случая диагностики [197]. ЭВМ задает исходные условия и предлагает обучаемому указать вид игры (стандартная, усложненная, ускоренная и облегченная). Допустим, выбрана усложненная игра. От обучаемого требуется в этом случае показать понимание технологической ситуации и ее многомерности. Затем ЭВМ просит обучаемого найти причину отклонения. В случае правильной диагностики в рамках заданного лимита времени ЭВМ фиксирует победу обучаемого.
Если же правильное решение принято с опозданием, машина разрешает продолжить игру с добавкой времени. Отказ от добавки ведет к фиксации проигрыша и повтору игры для другой ситуации; согласие на дополнительное время увеличивает штрафные очки, что не ведет к чистой победе, но и не исключает ничью. К ничьей ведет также правильное решение, принятое вовремя, но с помощью ЭВМ. Проигрыш фиксируется в случае ошибки обучаемого. От проигрыша следует отличать поражение, которое засчитывается обучаемому, если он принял ошибочное решение, отягощенное просрочкой времени, невзирая на помощь. Поражение вводит в действие дополнительные игры. Они делятся на две группы: игры с признаками и игры с причинами (табл. 9.1).
Из игр с признаками особенно существенной является игра «Найти приборы». Речь идет о проверке «прочности» связей между наименованиями признака и его индикаторами. В каждой группе дополнительных игр предусмотрены взаимные переходы. Что касается игр с причинами, то здесь особенно интересна игра «Очистить». Проведенные эксперименты с операторами электростанций показали особую трудность указанной фильтрации даже для опытных операторов. Игра состоит в максимально быстром выделении ложных причин, причем количество баллов, получаемых игроком, тем больше, чем выше правдоподобие ложной причины [197].
Таблица 9.1 Дополнительные игры
| Тип | Наименование | Краткое описание |
| Игры с признаками | Найти признаки | Задается частная ситуация; необходимо найти хотя бы один, несколько или все релевантные признаки |
| Найти приборы | Задаются признаки; необходимо найти прямые и косвенные их индикаторы | |
| Найти действие | Задаются признаки; необходимо определить диагностические действия, проявляющие их, и оценить влияние этих действий на основной процесс | |
| От признаков к причине | Задаются неупорядоченно признаки; необходимо организовать их в логические группы и маршруты вывода (заключения) | |
| Игры с причинами | Дополнить | Задается неполный перечень причин; требуется дополнить его |
| Упорядочить | Задаются неупорядоченные причины; требуется построить дерево оценки ситуаций | |
| Очистить | Часть заданных причин — ложная; требуется отделить их от истинных причин | |
| От причины к признакам | Игра отличается от позиции «Найти признаки» тем, что требуется указать относительную важность признаков |
Как уже отмечалось ранее, деловые игры находят широкое применение и при отработке управленческих решений по инженерно-психологическому (эргономическому) обеспечению новых образцов техники. Один из вариантов такой игры описан в [199]. В ней моделируется организация взаимодействия предприятия промышленности (заказчика) и разработчика по организации работ по инженерно-психологическому (эргономическому) обеспечению разработки, испытаний и внедрению новой техники.
Из рассмотренных примеров видно, что физическое имитационное моделирование, осуществляемое в форме деловых и учебных игр, направлено не только на исследование и изучение оперативной и управленческой деятельности, но и на обучение и тренировку оперативного и управленческого персонала, отработку ими соответствующих навыков и умений. В этом плане деловые игры выступают не столько как элемент исследовательской деятельности, сколько они являются одной из форм обучения и тренировок персонала.
9.2. Цифровая (статистическая) имитация
деятельности оператора
Рассмотренные ранее методы в ряде случаев не могут быть использованы для изучения и анализа деятельности оператора. Укажем некоторые из этих случаев.
1. Применение математических методов в процессе проектирования СЧМ, как правило, позволяет лишь приближенно оценивать деятельность оператора, поскольку эти методы не позволяют учесть целый ряд особенностей деятельности оператора. Попытки учета этих особенностей приводят к существенному усложнению модели. При этом может получиться, что аналитическое решение задачи оказывается либо принципиально невозможным, либо связанным с большими теоретическими и вычислительными трудностями.
2. Применение экспериментальных методов в процессе испытаний и эксплуатации СЧМ также не всегда оказывается возможным. Это может быть связано с опасностью для здоровья или жизни людей, невозможностью экспериментального воспроизведения некоторых ситуаций, с большой сложностью или стоимостью эксперимента.
В этих случаях весьма полезные результаты дает применение статистического моделирования. Оно базируется на методе статистических испытаний (метод Монте-Карло). Метод основан на розыгрыше (имитации) воздействия случайных факторов на деятельность оператора и функционирование СЧМ непосредственно в ходе моделирования. Этим объясняется другое название метода — имитационное моделирование.
Смысл метода заключается в многократной реализации с помощью ЭВМ моделируемого процесса. Каждая реализация носит случайный характер. Достоверность окончательного решения достигается статистической обработкой промежуточных результатов по множеству реализации.
Из этого следует, что имитационные методы занимают промежуточное положение между экспериментальными и математическими методами. По способу получения данных о деятельности оператора метод является математическим, а по характеру их получения и использования он копирует экспериментальный метод. Поэтому имитационные методы называют также машинным или математическим экспериментом.
Применение имитационных методов позволяет избежать многих недостатков экспериментальных и математических методов. С одной стороны, имитационные методы позволяют получить сравнительно высокую достоверность результатов моделирования уже на ранних этапах проектирования СЧМ. С другой стороны, по выражению академика В.М. Глушкова, математический эксперимент работает и в тех случаях, когда эксперименты с реальными объектами сильно затруднены, а порой и вовсе невозможны [29]. Кроме того, в ряде случаев его стоимость может оказаться гораздо ниже, чем стоимость эксперимента.
В настоящее время метод имитационного моделирования широко используется в различных областях. Применение его в инженерной психологии имеет ряд особенностей [54, 98, 215].
1. В основании имитационного моделирования СЧМ лежит представление о производственной деятельности оператора как совокупности отдельных действий. Последовательность этих действий должна быть известна (однозначно или в вероятностном плане). При этом предполагается, что в пределах заданных ограничений операторы будут действовать согласно предписаниям. Эти предписания могут быть детерминированными или вероятностными.
2. Описание каждого действия предельно упрощено: задается вероятность и время его выполнения, учитываются обобщенные показатели эффективности (качество выполнения, стоимость и др.). Психические процессы, регулирующие выполнение отдельного действия, при этом, как правило, не рассматриваются. Такое упрощение имеет определенное преимущество, поскольку позволяет отчетливее проследить внешние связи и взаимную согласованность отдельных действий, выявить влияние фактора времени, способствуя обнаружению основных источников изменения эффективности СЧМ.
3. Многие характеристики деятельности оператора носят вероятностный характер. Поэтому введение в модель элемента случайности резко повышает ее эффективность, так как позволяет получить не только детерминированные оценки результатов деятельности оператора, но и их законы распределения.
4. Отличительной чертой моделей СЧМ по сравнению с другими имитационными моделями является упор на использование и учет внешних проявлений психологических факторов. Наряду с данными о работе технических устройств модель учитывает такие переменные, как появляющееся временами состояние напряженности, квалификация и моральные качества отдельных операторов, спаянность коллектива и его направленность [54]. Представляется возможным также учет таких психологических характеристик, как особенности памяти оператора, его реакция, эмоциональная устойчивость, способность к взаимодействию с другими операторами и т.п. [45, 70]. Однако, поскольку число факторов, влияющих на эффективность деятельности оператора, очень велико и все их учесть одновременно невозможно, очень важно выбрать из них лишь самые существенные и отбросить малозначительные. Выбранные факторы должны быть представлены в такой форме, которая позволяет
5. осуществить имитацию их на ЭВМ и произвести соответствующую обработку полученных данных. 5. Меняя порядок выполнения отдельных действий, число операторов, их психофизиологические характеристики, условия работы и т. п., модель позволяет получить такие суммарные показатели качества работы, как относительное число решенных задач, время их решения, среднее время простоя операторов или время их перегрузки, вероятность выполнения системой предписанных функций и др. Сопоставляя полученные результаты, можно выбрать оптимальный вариант построения СЧМ. Следовательно, модель является удобным способом для сравнительной оценки различных вариантов построения системы.
Построение имитационных моделей базируется на применении научных данных из общей и групповой психологии, технических наук, математики, планирования эксперимента, практики применения ЭВМ. Структура модели определяется составом входящих в нее блоков и связями между ними. Такими блоками обычно являются: блок имитации средств и условий деятельности, блок имитации собственно деятельности и общения, блок генерации проблем (задач), блок определения и задания начальных условий, блок регистрации и обработки результатов моделирования, блок управления моделью. Конкретная структура модели определяется видом моделируемой задачи.
Имитационные модели деятельности оператора в системе «человек-машина» молено разбить на два основных вида: модели решения оператором отдельной конкретной задачи и модели его функционирования в условиях потока таких задач (модели обслуживания).
Модель первого вида рассмотрим на частном примере применения ее для определения времени решения задачи оператором. Для этого деятельность оператора представляется в виде суммы n отдельных независимых последовательно выполняемых действий. Для каждого из этих действий Должны быть известны законы распределения времени их выполнения. В соответствии с заложенной в память ЭВМ программой она формирует по заданному закону время выполнения первого действия t1, затем время t2 и т. д., пока не будет сформировано время выполнения последнего, n-го действия. Общее время решения задачи находится как сумма от tt до tn.
Процесс повторяется N раз, в результате чего получается N значений времени топ. По этим значениям строится закон распределения и вычисляются его основные характеристики τоп и στ.
При необходимости модель может учитывать и ошибки в выполнении отдельных действий. Для этого в память ЭВМ вводятся значения Р; — вероятности безошибочного выполнения i-ro действия (i = 1, 2...п). На каждом шаге ЭВМ вычисляет время ti и по жребию, в соответствии с вероятностью Р;, проверяет безошибочность выполнения i-ro действия. При наличии ошибки в зависимости от принятой программы работы это действие повторяется вновь либо повторяется все или часть предшествующих действий. Выполнение той или иной программы обусловлено характером исследуемой деятельности.
Модель будет еще более полной, если различать индивидуальные характеристики операторов, временные ограничения, налагаемые на процесс решения задачи, вводить различную срочность выполнения отдельных действий и т. д. Программа моделирования может быть представлена схемой, изображенной на рис. 9.1.
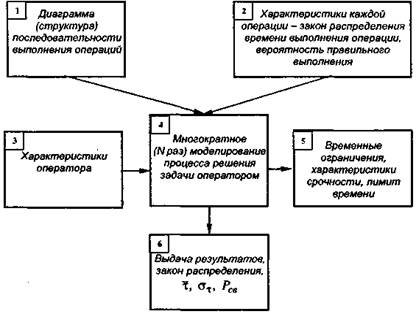 |
Рис. 9.1. Структурная схема имитационной модели деятельности оператора.
Блоки 1, 2, 3, 4 осуществляют ввод исходных данных, блок 5 проводит собственно моделирование заданное число N раз. По результатам N реализаций блок 6 вычисляет и выдает на печать закон распределения времени выполнения задачи, его числовые характеристики τоп и στ; вероятность своевременного выполнения задачи; части задачи, при выполнении которых оператор был недогружен или, наоборот, у него возникал дефицит времени, и другие величины.
В моделях второго вида (моделях обслуживания) характеристики решения оператором отдельных задач считаются известными. Здесь они выступают не как результат моделирования (как в первом случае), а в качестве исходных данных. Кроме этого, исходными данными являются:
■ поток задач, решаемых оператором (моменты поступления задач, их характер, приоритет и т. д.);
■ поток ошибок оператора (моменты или вероятности возникновения ошибок, их последействие, время исправления и т. п.);
■ индивидуальные психофизиологические характеристики операторов, оказывающие влияние на их деятельность;
■ особенности протекания процесса управления (например, временные ограничения в системе «человек-машина».
На первом этапе моделирования проводится формализованное описание деятельности оператора. После этого строится математическая модель, т. е. деятельность оператора описывается с помощью математических объектов (формул, уравнений, неравенств). Для моделирования на ЭВМ модель преобразуется в моделирующий алгоритм, на основании которого составляется программа моделирования.
Более подробно эти задачи выглядят так. При формализации деятельности оператора могут быть учтены многие психофизиологические закономерности операторской деятельности: недоступность обслуживания, процессы памяти, возникновение напряженности и утомления, возникновение ошибок и их исправление, взаимодействие операторов, динамика работоспособности и др. [168].
Недоступность обслуживания обусловлена периодами недоступности, наличие которых объясняется тем, что часть рабочего времени оператора представляется ему для отдыха, кроме того, у него могут быть и иные обязанности, непосредственно не связанные с обслуживанием поступающей информации. Периоды недоступности задаются законом распределения и вероятностью появления их в течение определенного промежутка времени.
При описании процессов памяти рассматриваются основные процессы, связанные с хранением и воспроизведением информации. В этих процессах участвуют два вида памяти: долговременная и кратковременная. Любая поступающая информация поступает в кратковременную память, имеющую определенный объем k0. Информация сохраняется в течение времени, не превышающего длительность следа кратковременной памяти.
Информация, вытесненная из кратковременной памяти, с определенной вероятностью направляется в долговременную память либо теряется. Информация, находящаяся в кратковременной памяти, а также направленная в долговременную, воспроизводится полностью и без потерь. Однако время обслуживания в последнем случае увеличивается на величину τп — время поиска информации в долговременной памяти, или время обращения к долговременной памяти. Вероятность потери, вероятности обслуживания кратковременной и долговременной памятью, время поиска используются в качестве исходных данных и определяются либо экспериментально, либо расчетным путем с использованием моделей памяти [16].
Напряженность в работе оператора может быть двух типов: операциональная и эмоциональная. При формализации деятельности оператора учитывается обычно только операциональная напряженность, возникающая вследствие сложности выполняемой работы за пультом управления. Эмоциональная напряженность не
рассматривается из-за трудностей количественного описания степени напряженности такого вида.
При моделировании вводятся две степени состояния оператора: ненапряженное (нормальное) и напряженное состояние, которое является источником дополнительных ошибок.
Нормальное состояние имеет место, когда число поступивших сигналов не превышает объем кратковременной или оперативной памяти и не возникает дефицит времени при обработке информации. При нарушении любого из этих условий возникает напряженность. Условия возникновения этих состояний можно записать следующим образом:
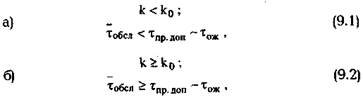
где τож — время ожидания начала обслуживания данного сигнала; τпр.доп — допустимое время пребывания сигнала на обслуживании, или лимит времени, отводимый на обслуживание данного сигнала. Очевидно, чем больше τож, тем меньше времени отводится для обслуживания.
Из выражений (9.1) и (9.2) следует, что дефицит времени возникает тогда, когда оператор видит, что оставшегося времени (τдоп — τож) ему не хватит для своевременной обработки сигнала, если он будет работать с нормальной скоростью. Это требует от него более интенсивной (т. е. напряженной) работы и связано обычно с увеличением числа ошибок.
Взаимодействие операторов в процессе обслуживания поступающей информации может оказать как положительное, так и отрицательное влияние на результаты деятельности исследуемого оператора. Положительное влияние проявляется в возможности дублирования (резервирования) работы оператора. Резервирование приводит к уменьшению вероятности совершения ошибки при некотором увеличении времени обслуживания.
Отрицательное влияние взаимодействия заключается в выполнении оператором дополнительной работы, связанной с контролем действий других операторов, проверкой получаемых от них данных, ответами на запросы, исправлением их ошибок и т. д. Для учета этого во входящий поток вводится дополнительный поток требований, обусловленный взаимодействием.
При рассмотрении динамики работоспособности оператора учитывается влияние «вхождения» в работу (врабатываемости) и утомления. Для учета этих явлений основные характеристики деятельности оператора задаются в функции времени его работы за пультом управления. Эта функция графически изображена на рис. 4.9.
Для учета возможности совершения оператором ошибочных действий и их исправления требуется решение нескольких задач: моделирование события «возникновение ошибки», решение вопроса о судьбе сообщения, при обслуживании которого было допущено ошибочное действие; учет последействия потока ошибок.
Моделирование ошибок заключается в следующем. В результате экспериментальных исследований определяется вероятность совершения ошибки ρош, после чего по жребию выбирается соответствующий результат для получения события «возникновение ошибки при обслуживании данного сообщения». Это имеет место при выполнении условия
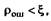 (9.3)
(9.3)
где 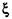 — число, равномерно распределенное в интервале [0, 1], вырабатываемое ЭВМ.
— число, равномерно распределенное в интервале [0, 1], вырабатываемое ЭВМ.
В процессе решения вопроса о судьбе требования, при обслуживании которого совершено ошибочное действие, обычно принимается следующий вариант: при совершении ошибки обслуживание прекращается и возобновляется только после ее исправления.
Последействие потока ошибок определяет взаимную зависимость вероятностных характеристик потока для двух непересекающихся между собой интервалов времени. С целью введения последействия ρош задается как функция длины очереди. При этом последействие проявляется в том, что совершение ошибки и необходимость ее исправления приводят к увеличению длины очереди, а следовательно, и к увеличению вероятности ошибки при обслуживании последующих требований. Проведенные исследования показывают, что зависимость ρош = f (k) носит линейный характер.
Для моделирования на ЭВМ необходимо преобразовать построенную модель исследуемого процесса (процесса функционирования оператора) в специальный моделирующий алгоритм, в соответствии с которым в машине вырабатывается информация, описывающая элементарные явления исследуемого процесса с учетом их связей и взаимных влияний. Укрупненная структурная схема алгоритма приведена на рис. 9.2.
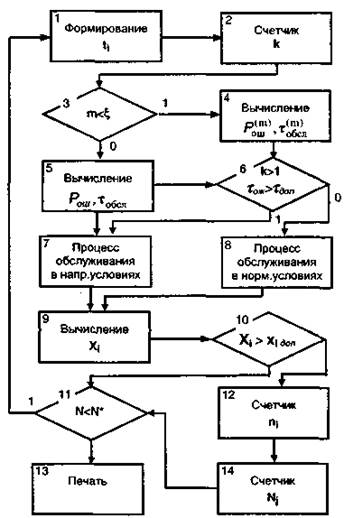
Рис. 9.2. Структурная схема имитационной модели обслуживания.
В соответствии с принятыми обозначениями арифметические блоки изображены прямоугольниками, логические — ромбами. Если условие, проверяемое логическим блоком, выполнено, то управление передается по стрелке с индексом 1, в противном случае — по стрелке с индексом 0.
Принцип работы схемы заключается в следующем. Блок 1 формирует моменты поступления tj очередных сообщений в соответствии с заданным законом распределения. Блок 2 производит подсчет числа k сообщений, одновременно находящихся на обслуживании. Блок 3 проверяет условие ρсов<ξ, (где ρсов — вероятность совместного обслуживания двумя операторами). Выполнение этого условия свидетельствует о наличии резервирования при обслуживании данного сообщения.
Блоки 4 и 5 производят вычисление основных характеристик деятельности оператора. Эти характеристики различны при резервировании и отсутствии резервирования и являются функциями от длины очереди и времени. Блок 6 проверяет условия возникновения напряженности в соответствии с выражениями (9.1) и (9.2). В зависимости от результатов этой проверки блоки 7 и 8 моделируют процесс обслуживания в нормальных и напряженных условиях.
Блок 9 подсчитывает количество проделанных реализаций N*, а блок 10 сравнивает его с числом N — количеством реализаций, необходимым для достижения заданной точности моделирования. При N*<N моделирование продолжается, при N*=N — заканчивается и блок 11 выдает результаты моделирования на печать. В зависимости от целей моделирования на печать могут быть выданы различные характеристики моделируемого процесса: вероятностные характеристики очереди и времени ожидания, продолжительность пауз между обслуживанием сообщений и т. д.
С их помощью вычисляются многие характеристики деятельности оператора: степень загрузки, периоды занятости, своевременность решения задач и др. Зная их, можно определить допустимую плотность (темп поступления) задач, произвести оценку загрузки оператора, выявить характер и частоту появления различных ситуаций в системе «человек-машина».
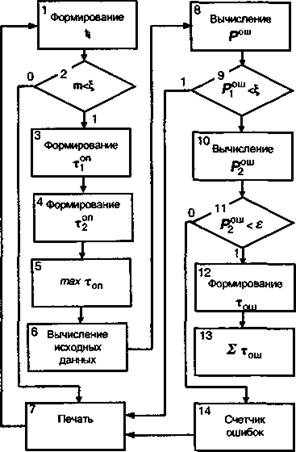
Рис. 9.3. Структурная схема имитационной модели групповой деятельности.
Схема моделирующего алгоритма (рис. 9.2) носит самый общий характер и показывает лишь общий принцип построения имитационной модели обслуживания. В более подробном виде она произведена в [45, 70]. Кроме этого на основе общей схемы могут быть построены и некоторые частные схемы: моделирования групповой деятельности (рис. 9.3), моделирования процесса обслуживания разнородных заявок, моделирования напряженности в работе оператора и др. [45, 173].
Как отмечалось в начале главы, имитационное моделирование может быть аналитическим и статистическим. Приведенные на рис. 9.1 и 9.2 схемы алгоритмов реализуют идею статистического моделирования, осуществляемого методом статистических испытаний. При аналитическом имитационном моделировании (АИМ) как весь алгоритм, так и отдельные единицы функционирования описываются аналитическими моделями. Идея АИМ возникла в рамках теории функциональных сетей. Этот вид моделирования был выбран по следующим соображениям: аналитическое моделирование является более предпочтительным с точки зрения точности результатов моделирования; оно лишено главных недостатков статистического моделирования — необходимости проведения значительного числа реализаций и статистической обработки результатов. Для реализации АИМ разработан специальный язык АЯТС (алгоритмический язык типовых структур) и специальное программное обеспечение, позволяющее осуществить представление функциональной сети с помощью этого языка [137]. Однако функциональные возможности и область практического применения АИМ намного уже, чем у статистического имитационного моделирования.

 2015-10-13
2015-10-13 3224
3224
