Методические указания по выполнению лабораторных и расчетно-графических работ
Лабораторная работа №1. Методы интерполяции.
Задание. Протабулировать произвольно заданную нелинейную функцию  на отрезке
на отрезке  с постоянным шагом
с постоянным шагом  , где n – число точек (узлов) таблицы n = 4…10. По результатам табулирования функции
, где n – число точек (узлов) таблицы n = 4…10. По результатам табулирования функции  построить таблицу
построить таблицу

| 
| 
| … | 
|

| 
| 
| … | 
|
Используя линейную и квадратичную интерполяцию, вычислить значения функции в двух произвольных, не лежащих в узлах таблицы, точках 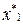 и
и 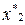 , в которых функция имеет разную кривизну. Вычислить в процентах относительную погрешность интерполяции по отношению к точному значению функции в точках
, в которых функция имеет разную кривизну. Вычислить в процентах относительную погрешность интерполяции по отношению к точному значению функции в точках 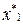 и
и 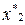 , и сделать соответствующие выводы.
, и сделать соответствующие выводы.
Решение.
Пусть функция имеет вид  – т.е. многочлен четвертого порядка. (Если выбранная функция – многочлен, то порядок его должен быть задан выше двух, иначе при использовании квадратичной интерполяции получим абсолютно точный результат). Протабулируем функцию на отрезке
– т.е. многочлен четвертого порядка. (Если выбранная функция – многочлен, то порядок его должен быть задан выше двух, иначе при использовании квадратичной интерполяции получим абсолютно точный результат). Протабулируем функцию на отрезке  с постоянным шагом
с постоянным шагом  , где n=4 – число точек (узлов) таблицы. По результатам табулирования функции
, где n=4 – число точек (узлов) таблицы. По результатам табулирования функции  построим таблицу 1.1 и график функции (рисунок 1.1)
построим таблицу 1.1 и график функции (рисунок 1.1)
Таблица 1.1

| 
| 
| 1,25 | 
|

| 
| 
| 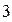
|

Рисунок 1.1 График функции 
Выберем две точки  и
и  , в которых функция имеет разную кривизну.
, в которых функция имеет разную кривизну.
1.1 Расчеты в точке 
Вычислим точное значение функции в этой точке: 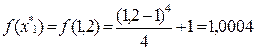 .
.
Вычислим значение функции, используя формулы линейной интерполяции:
 , т.е.
, т.е.
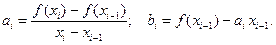
Точка  находится между узлами
находится между узлами  и
и  . В этом случае
. В этом случае



Относительная погрешность линейной интерполяции в процентах равна
 .
.
Вычислим теперь значение функции в точке  , используя формулы квадратичной интерполяции. Найдем приближенное значение функции с помощью формулы квадратичной интерполяции
, используя формулы квадратичной интерполяции. Найдем приближенное значение функции с помощью формулы квадратичной интерполяции
 .
.
Для нахождения коэффициентов  составим систему уравнений (2.14) (смотри теоретический материал)
составим систему уравнений (2.14) (смотри теоретический материал)

Так как точка  ближе к узлу
ближе к узлу  , чем к узлу
, чем к узлу  , то выбираем для расчета следующие три узла:
, то выбираем для расчета следующие три узла:  ,
,  ,
,  . Соответственно
. Соответственно  ,
, 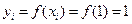 ,
,  .
.
Тогда система запишется в виде:

Решая эту систему, находим  . Искомое значение функции
. Искомое значение функции  .
.
Относительная погрешность квадратичной интерполяции в процентах равна
 .
.
1.2 Расчеты в точке с большей кривизной 
Вычислим точное значение функции в этой точке:  .
.
Вычислим значение функции, используя формулы линейной интерполяции:
 , т.е.
, т.е.
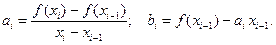
Точка  находится между узлами
находится между узлами  и
и  . В этом случае
. В этом случае


 .
.
Относительная погрешность линейной интерполяции в процентах равна

Вычислим теперь значение функции в точке  , используя формулы квадратичной интерполяции. Найдем приближенное значение функции с помощью формулы квадратичной интерполяции
, используя формулы квадратичной интерполяции. Найдем приближенное значение функции с помощью формулы квадратичной интерполяции
 .
.
Для нахождения коэффициентов  составим систему уравнений (2.14) (смотри теоретический материал)
составим систему уравнений (2.14) (смотри теоретический материал)

Так как точка  ближе к узлу
ближе к узлу  , чем к узлу
, чем к узлу  , то выбираем для расчета следующие три узла:
, то выбираем для расчета следующие три узла:  ,
,  ,
,  . Соответственно
. Соответственно  ,
,  ,
,  .
.
Тогда система запишется в виде:

Решая эту систему, находим  . Искомое значение функции
. Искомое значение функции  .
.
Относительная погрешность квадратичной интерполяции в процентах равна
 .
.
Проверка проведенных вычислений по компьютерной программе




 2015-10-22
2015-10-22 614
614







