ВИДЫ механического движения

ВВЕДЕНИЕ

1. ПРЕДМЕТ ФИЗИКА

1.1. Что изучает физика?

Физика — это наука о природе. Физика изучает физические тела, физические процессы и физические явления.

Например:

— стол, дом, Солнце, вода, воздух — это физические тела;

—камень падает — это физический процесс;

—автобус движется — это физический процесс;

—идёт дождь — это физическое явление.

физика	physics	physique	fisica
изучать	study	étudier	estudiar
природа	nature	nature	naturaleza
тело	body	corps	cuerpo
процесс	process	processus	proceso
явление	phenomenon	phenomène	phenómeno

1.2. Физическая величина

Ф и з и ч е с к а я в е л и ч и н а — это характеристика физического тела, физического процесса, физического явления.

Пример (рис. 1). Это тело. Тело имеет массу, длину, объем. Длина, масса, объем — это характеристики тела.

Длина, масса, объем — это физические величины.

Пример (рис. 2). Это автобус. Автобус движется.

Скорость автобуса равна 60 км/ч (шестидесяти километрам в час).

Скорость — это характеристика движения (характеристика физического процесса).

Скорость — это физическая величина.

Физические величины мы обозначаем буквами латинского алфавита и греческого алфавита, например:

— массу мы обозначаем буквой m (читаем «эм»),

— длину мы обозначаем буквой ℓ (читаем «эль»),

— время мы обозначаем буквой t (читаем «тэ»),

— плотность мы обозначаем буквой ρ (читаем «ро»).

физическая величина	physical quantity	grandeur physique	magnitude física
характеристика	characteristic	caractéristique	caracteristica
движение	motion	mouvement	movimiento
длина	length	longueur	longitud
масса	mass	masse	masa
время	time	temps	tiempo
обозначать	designate	désigner	señalar

1.3. Методы определения физических величин

Как мы можем найти физическую величину? Физическую величину мы можем измерить.

Пример (рис. 3).

1. Длину тела ℓ мы измеряем линейкой (рис. 3, а). Линейка — это прибор для измерения длины.

2. Массу тела m мы измеряем на весах (рис. 3, б). Весы — это прибор для измерения массы.

3. Время t мы измеряем секундомером (рис. 3, в). Секундомер (часы) — это прибор для измерения времени.

Таким образом, длину, массу, время мы измеряем измерительными приборами.

Физическую величину мы можем найти по формуле.

Пример (рис. 4). Тело имеет форму параллелепипеда. Объем параллелепипеда мы определяем по формуле.

V = ℓ·d· b.

Рис. 3

Длину ℓ, ширину b, толщину d мы измеряем линейкой.

Если мы знаем массу тела m и объем V, то мы можем найти плотность вещества ρ (читаем «ро») по формуле

Мы можем найти по формулам и другие физические величины, например скорость, силу, работу.

С д е л а е м в ы в о д ы:

1) физическую величину мы можем измерить физическим прибором;

2) физическую величину мы можем найти по формуле.

метод	method	méthode	methodó
найти	find	trouver	encontrar
измерить	measure	mesurer	medir
прибор	device	appareil	aparato
шкала	scale	échelle	escala
линейка	roule	règle	regla
весы	balance	balance	pesa
секундомер	stop-watch	chronomètre	chronómetro
формула	formula	formula	formula
объём	volume	volume	volumen
плотность	density	densité	densidad
вещество	matter	matière	substancia
сделать вывод	make a conclusion	faire une conclusion	sacar conclusiones
толщина	thickness	épaisseur	gordura
ширина	width	largeur	anchura
высота	height	hauteur	altura
сила	force	force	fuerza
скорость	velocity	vitesse	velocidad
работа	work	travail	trabajo

1.4. Единицы измерения физических величин

Е д и н и ц ы д л и н ы

Основные единицы измерения

1 м (один метр), 1 см (один сантиметр), 1 мм (один миллиметр), 1 км (один километр) ¾ это единицы длины.

1 км = 1000 м (один километр равен тысяче метров),

1 м = 100 см (один метр равен ста сантиметрам),

1см = 10 мм (один сантиметр равен десяти миллиметрам).

Единица измерения обозначается символом физической величины в квадратных скобках:

[ ℓ ] = 1 м, [ ℓ ] = 1 см, [ ℓ ] = 1 км.

Е д и н и ц ы м а с с ы

1 кг (один килограмм), 1 г (один грамм),

1 т (одна тонна) — это единицы массы.

[ m ] = 1 кг, [ m ] = 1 г, [m ] == 1 т.

1 т = 1000 кг (в одной тонне — тысяча килограммов),

1 кг = 1000 г (в одном килограмме — тысяча граммов),

1 г =1000 мг (в одном грамме — тысяча миллиграммов).

Е д и н и ц ы в р е м е н и

1 ч (один час), 1 мин (одна минута), 1 с (одна секунда) — это единицы времени.

[ t ] = 1 ч, [ t ] = 1 мин., [t ] = 1 с.

1 ч = 60 мин (один час равен шестидесяти минутам),

1 мин. = 60 с (одна минута равна шестидесяти секундам),

1 ч = 3600 с (один час равен трём тысячам шестистам секундам).

Производные единицы измерения

Единицы измерения физических величин, которые мы определяем по формулам, — это производные единицы измерения.

Рассмотрим некоторые производные единицы измерения.

Е д и н и ц ы о б ъ ё м а

Формула объема параллелепипеда V = ℓ·b·d. В этой формуле ℓ, b и d измеряются в единицах длины, например в метрах или в сантиметрах. Тогда единицы объема:

[V ] = [ ℓ ] ³.

[ V ] = l м³ (один кубический метр) или [ V ] =1 см³ (один кубический сантиметр).

Е д и н и ц ы п л о т н о с т и

Формула плотности вещества .

Если масса измеряется в килограммах, а объём — в кубических метрах, то единица плотности

1кг/м³ (один килограмм на кубический метр).

Единицы измерения объема, плотности, скорости, силы, работы и других физических величин — это производные единицы.

единица измерения	unit of measurement	unité de mesure	unidad medida
основная единица	basic unit	unité de base	unidad básica
производная единица	derived unit	unité dérivée	unidad derivada
символ	symbol	symbole	símbolo
подставить	substitute	mettre	meter

1.5. Система единиц

Система единиц состоит из основных и производных единиц.

Международная система единиц (СИ)

Основные механические единицы в СИ:

единица длины [ ℓ ] = 1 м — один метр,

единица массы [ m ] = 1 кг — один килограмм,

единица времени [ t ] = 1 с — одна секунда.

Единицы измерения других физических

величин — производные единицы:

единица скорости [υ] = 1 м/с — один метр в секунду,

единица ускорения [ а ] = 1 м/с² — один метр на секунду в квадрате,

единица силы [ F ] — 1 кг·м/с²= 1 Н — один ньютон,

единица работы [ А ] = 1 Н·м = 1 Дж — один джоуль,

единица плотности [ρ] = 1 кг/м³ — один килограмм на кубический метр.

Основные механические единицы в СГС:

Физическая система единиц ( СГС)

единица длины [ ℓ ] = 1 см (один сантиметр),

единица массы [ m ] = 1 г (один грамм),

единица времени [ t ] = 1 с (одна секунда).

Некоторые производные единицы в СГС:

единица скорости [ υ ] = 1 см/с,

единица ускорения [ а ] = 1 см/с²,

единица силы [ F ] = 1 г×см/с²= 1 дин — одна дина,

единица работы [ А ] = 1 дин·см = 1 г×см ²/с² = 1 эрг.

Мы можем переводить единицы измерения из одной системы единиц в другую. Например, единица плотности в СИ [ρ] = 1 кг/м³. Найдем значение этой единицы в системе СГС:

1 кг/м³= 1 кг/1м³= 10³г/10⁶см³= 10^-3 г/см³.

??? ОТВЕТЬТЕ НА ВОПРОСЫ:

1. Что изучает физика?

2. акие физические тела вы знаете?

3. Какие физические величины вы знаете?

4. Каким прибором мы измеряем длину?

5. Какую физическую величину измеряют секундомером?

6. Сколько сантиметров в одном километре?

7. Сколько секунд в одном часе?

система единиц	system of units	système dˊunités	sistema de unidad
Международная система (СИ)	International System	Système International	Systema Internacional
значение	value	valeur	valor
переводить единицы	transform units	convertir des unités	transformar unidades
система СГС	system CGS	système CGS	systema CGS

2. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ВЕЛИЧИНЫ

2.1. Скалярные величины

С к а л я р н а я в е л и ч и н а — это физическая величина, которая имеет численное значение и единицу измерения.

Скалярная величина может быть положительной или отрицательной.

Примеры скалярных величин: температура, масса, объём, время, плотность. Математические действия со скалярными величинами — это алгебраические действия с числами.

2.2. Векторные величины

В е к т о р н а я в е л и ч и н а — это физическая величина, которая имеет:

1) численное значение, которое всегда положительно (модуль вектора);

2) направление;

3) единицу измерения.

Примеры векторных физических величин: скорость, ускорение, сила.

Векторная величина обозначается буквой и стрелкой над этой буквой. Например:

— вектор скорости обозначается символом ,

— вектор ускорения обозначается символом ,

— вектор силы обозначается символом .

Модуль вектора обозначается так:

½ ½ или υ — модуль вектора ,

½ ½ или а — модуль вектора ,

| | или — модуль вектора .

На рисунке (графически) вектор изображается направленным отрезком прямой линии (рис. 5). Модуль вектора равен длине отрезка в зáданном масштабе (рис. 6).

скаляр	scalar quantity	grandeur scalaire	magnitude escalar
вектор	vector	vecteur	vector
численное значение	numerical value	valeur numerique	numeric valor
модуль	modul	module	modulo
направление	direction	direction	direccion
отрезок	segment	segment	segmento
стрелка	arrow, point	aiguille	aguja
масштаб	scale	échelle	escala
прямая линия	straight line	ligne droite	recta linea

3. ДЕЙСТВИЯ С ВЕКТОРАМИ

Математические действия с векторными величинами — это действия векторной алгебры.

3.1. Сравнение векторов

Рассмотрим два вектора и (рис. 7).

Равные векторы. ( = ). Два вектора равны, если они имеют:

— равные модули,

— одинаковые направления.

Равнопротивоположные векторы. ( = - ). Два вектора равнопротивоположны, если они имеют:

— равные модули,

— противоположные направления.

3.2. Сложение векторов

Мы можем сложить два вектора геометрически по правилу параллелограмма и по правилу треугольника.

Пусть заданы два вектора и (рис. 8).

Найдём сумму этих векторов

Векторы и — это составляющие векторы, вектор — это результирующий вектор.

Правило параллелограмма для сложения двух векторов:

1. Нарисуем вектор .

2. Нарисуем вектор так, чтобы его начало совпадало с началом вектора ; угол между векторами равен a (альфа).

3. Через конец вектора проведём
прямую линию, параллельную вектору .

4. Через конец вектора проведём

прямую линию, параллельную вектору . Мы построили параллелограмм. Стороны этого параллелограмма — составляющие векторы и .

5. Проведем диагональ параллелограмма из общей точки начала вектора и начала вектора .

6. Модуль результирующего вектора
равен длине диагонали параллелограмма
и определяется по формуле

начало вектора совпадает с началом вектора и началом вектора (направление вектора показано на рисунке).

Правило треугольника для сложения
двух векторов (рис. 9):

1. Нарисуем составляющие векторы
и так, что начало вектора совпадает
с концом вектора . При этом угол между сторонами треугольника равен b (бета).

2. Результирующий вектор — это вектор, начало которого совпадает с началом вектора , а конец совпадает с концом вектора .

Модуль результирующего вектора находим по формуле

3.3. Вычитание векторов

Пусть заданы два вектора и ;угол между векторами равен a (альфа) (рис. 10, а). Найти вектор

. В этом выражении

вектор —вектор разности;

вектор — уменьшаемый вектор;

вектор — вычитаемый вектор.

Модуль вектора разности определяется по формуле

Найти разность вектора и вектора — это то же самое, что найти сумму вектора и вектора (- ) противоположного вектору :

Мы можем найти (изобразить) вектор разности геометрически по правилу параллелограмма или по правилу треугольника (рис. 10).

Правило параллелограмма. Стороны параллелограмма — вектор и вектор (- ); диагональ параллелограмма — вектор разности (рис. 10, б).

Правило треугольника.

Вариант 1. Если начало уменьшаемого вектора (вектора ) и начало вычитаемого вектора (вектор ) находятся в одной точке (совпадают), то вектор разности направлен из конца вычитаемого вектора в конец уменьшаемого вектора (рис. 10, в)

Вариант 2. Вектор разности соединяет начало вектора и конец вектopa (- ) (начало вектора (- ) совпадает с концом вектора ) (рис. 10, г).

3.4. Умножение вектора на скаляр

Пусть заданы вектор и скаляр n. Найдём произведение вектора и скаляра n.

В результате умножения вектора на

скаляр мы получаем новый вектор :

= n · (рис. 11).

Направление вектора такое же, как направление вектора при n > 0.

Направление вектора противоположно направлению вектора при n < 0.

Модуль вектора в n раз больше модуля вектора , если n >1.

3.5. Разложение вектора на составляющие

Разложить вектор на составляющие векторы по двум зáданным направлениям — это значит найти два вектора и :

— направления которых совпадают c зáданными направлениями;

— сумма которых равна вектору .

Геометрически разложить вектор на составляющие векторы — это значит построить параллелограмм по зáданной диагонали и зáданным направлениям сторон.

Найдём составляющие вектора по зáданным направлениям АВ и CD. (рис. 12):

1. Через начало и конец вектора проводим прямые линии, параллельные одному из зáданных направлений (АВ).

2. Через начало и конец вектора проводим прямые линии, параллельные второ- му зáданному направлению (CD).

Мы построили парал- лелограмм.

Рис. 12

3. Зáданный вектор направлен по диагонали параллелограмма, построенного на искомых составляющих векторах и : Начала векторов , , находятся в одной точке.

3.6. Проекция вектора на оси координат

П р о е к ц и я в е к т о р а н а о с ь — это скалярная величина, равная произведению модуля вектора на косинус угла между направлением вектора и положительным направлением оси (рис. 13, а):

— это вектор;

c_х — это проекция вектора на ось ОХ;

c _у — это проекция вектора на ось ОУ;

a — это угол между вектором и осью ОХ;

b — это угол между вектором и осью OУ

Так как

(рис.13, а), то

На рис.13, б:

c_х — это графическое изображение проекции вектора на ось O X;

c _у — это графическое изображение проекции вектора на ось O У

Найдём проекции вектора на оси координат 0Х и 0У в прямоугольной (декартовой) системе координат (рис. 14, а, б, в, г) методом разложения вектора на составляющие:

1. Разложим вектор на два составляющих вектора и ;

— составляющий вектор по оси ОХ;

— составляющий вектор по оси ОУ.

2. Проекция вектора на ось ОХ равна модулю составляющего вектора со знаком «плюс» или «минус»:

c_х >0, если (рис. 14, а; рис. 14, г);

c_х < 0, если (рис. 14, б; рис. 14, в).

3. Проекция вектора на ось ОУ равна модулю составляющего вектора со знаком «плюс» или «минус»:

c_у >0, если (рис. 14, а; рис. 14, в)

с_у < 0, если (рис. 14, б; рис. 14, г)

Рассмотрим частные случаи

а б а б

Рис. 15 Рис. 16

Так как вектор и (рис. 15, а), то c_у = + с и c_х = 0

Так как вектор и (рис. 15, б), то c_у = - с и c_х = 0

Так как вектор и (рис. 16, а), то c_х = + с и c_у = 0

Так как вектор и (рис. 16, б), то c_х = - с и c_у = 0

Можно решить обратную задачу: если мы знаем проекции вектора, то

мы можем найти сам вектор, т. е. найти модуль вектора и направление

вектора (рис. 17).

Модуль вектора

Направление вектора определяют углы a и b:

Или из рис. 17 следует:

Зачем нам нужно знать проекции вектора? Так как проекции векторов на оси координат — это скалярные величины, мы можем заменить любое векторное равенство (уравнение) системой скалярных равенств (уравнений). При этом геометрические действия с векторами мы заменяем алгебраическими действиями с проекциями векторов.

!!! 3апомните правила: Проекция результирующего вектора (вектора суммы) на данную ось равна алгебраической сумме проекций составляющих (слагаемых) векторов на эту же ось:

;

Проекция вектора разности на данную ось равна разности проекций уменьшаемого и вычитаемого векторов на эту же ось.

;

??? ОТВЕТЬТЕ НА ВОПРОСЫ:

1. Какие векторные величины вы знаете?

2. Какие скалярные величины вы знаете?

3. В каком случае модуль результирующего вектора равен:

а) сумме модулей составляющих векторов?

б) разности модулей составляющих векторов?

4. Можно ли сказать, что , если:

, ?

5. В каком случае проекция вектора на ось координат:

а) положительная величина? б) отрицательная величина?

в) равна нулю? г) равна модулю вектора со знаком «+»?

д) равна модулю вектора со знаком «-»?

параллельные линии	parallel lines	lignes parallèles	lineas paralelas
противоположные векторы	opposite vectors	vecteurs de sens opposés	vectores anti-paralelos
геометрический	geometric	géométrique	geométrico
параллелограмм	parallelogram	parallèlogramm	paralelogramo
треугольник	triangle	triangle	triangulo
составляющий вектор	component vector	vecteur composant	vector componente
результирующий вектор	resulting vector	vecteur résultant	vector resultante
совпадать	coincide	coincider	coincidir
сторона	side	coté	lado
ось	axis	axe	eje
диагональ	diagonal	diagonal	diagonal
разложение	decomposition	décomposition	decomposicion
проекция	projection	projection	proyeccion
система координат	system of coordinates	système de coordonnées	sistema de coordinadas
перпендикуляр	perpendicular	perpendiculaire	perpendicular
прямоугольный	rectangular	rectangulaire	rectángulo

МЕХАНИКА

Механика изучает механическое движение.

М е х а н и ч е с к о е д в и ж е н и е — это процесс изменения положения тела относительно другого тела, которое мы условно считаем неподвижным и называем телом отсчёта.

Ⅰ. КИНЕМАТИКА

К и н е м a т и к а — это часть механики, которая изучает механическое движение, но не учитывает причины, вызывающие это движение.

Задача кинематики ¾ ввести физические величины, которые характеризуют механическое движение и установить соотношения между ними.

1. ОСНОВНЫЕ ПОНЯТИЯ И ХАРАКТЕРИСТИКИ КИНЕМАТИКИ

Мы изучаем движение материальной точки.

1.1. Материальная точка

М а т е р и а л ь н а я т о ч к а — это физическое тело, форму и размеры которого мы можем не учитывать в данной задаче.

Например: Земля движется вокруг Солнца. Размеры Солнца и Земли меньше, чем расстояние между Солнцем и Землёй. В этом случае мы можем считать, что Солнце и Земля — материальные точки.

1.2. Траектория

Т р а е к т о р и я — это линия, которую описывает материальная точка при движении (рис. 18).

а б

Рис. 18

Эта траектория (рис. 18, а) — кривая линия. Движение материальной точки к р и в о л и н е й н о е.

Эта траектория (рис. 18, б) — прямая линия. Движение материальной точки п р я м о л и н е й н о е.

1.3. Путь

П у т ь — это скалярная, всегда положительная физическая величина, которая равна длине траектории. Путь обозначается буквой S (читаем «эс»).

Путь измеряется в единицах длины.

Единица пути в СИ: [ S ] = 1 м.

Единица пути в системе СГС: [ S ] = 1 см.

Внесистемная единица пути: [ S ] = 1 км.

1.4. Время

Время — скалярная физическая величина. Момент времени обозначается символом t.

Интервал времени — это разность между двумя моментами времени.

Интервал времени обозначается символом Δ t (читаем «дельта тэ»):

Δ t = t – t ₀,

где t — это любой момент времени,

t ₀ — это начальный момент времени.

Единица времени в СИ и в системе СГС [ t ] = l с.

механика	mechanics	mécanique	mecánica
кинематика	kinematics	cinématique	cinemática
изменение	change	variation	cambio
положение	position	position	posición
относительно	relatively	relativementà	en relación
покой	rest	repos	reposo
материальная точка	material point	point matériel	point material
траектория	trajectory	trajectoire	trayectoria
путь	path	distance	camino
внесистемная единица	non-system unit	unité hors système	unidad fuera del sistema
момент времени	moment of time	moment du temps	momento de tiempo
интервал времени	interval of time	intervalle du temps	intervalo de tiempo

1.5. Тело отсчёта

Т е л о о т с ч ё т а — это тело, относительно которого мы рассматриваем движение данного тела.

По дороге движется автомобиль, в котором находится человек (рис. 19).

В о п р о с: движется или не движется человек?

О т в е т:

— человек движется относительно дерева (дерево — это тело отсчёта);

— человек не движется (находится в покое) относительно автомобиля (автомобиль — это другое тело отсчёта).

Мы видим, что человек движется относительно одного тела отсчёта (дерева) и не движется относительно другого тела отсчёта (автомобиля).

С д е л а е м в ы в о д: движение и покой — относительные состояния.

1.6. Система координат

Мы определяем положение материальной точки её координатами в выбранной нами с и с т е м е к о о р д и н а т (рис. 20). Точка О — это начало координат.

Положение точки на прямой линии определяет одна координата (см. рис. 20, а).

Положение точки на плоскости определяют две координаты (см. рис. 20, б).

Положение точки в пространстве определяют три координаты (см. рис. 20, в).

1.7. Система отсчёта

Мы изучаем движение тела в системе отсчёта (рис. 21).

Система отсчёта — это тело отсчёта + система координат, связанная с телом отсчёта + секундомер.

Тело отсчёта нужно, чтобы определить, движется данное тело или находится в покое в данной системе отсчёта.

Система координат нужна для определения положения тела относительно тела отсчёта.

Секундомер (часы) — это прибор для измерения времени.

тело отсчёта	body of reference	Corps de référence	cuerpo de referencia
система отсчёта	system of reference	système de référence	sistema de referencia

1.8. Радиус-вектор

Нарисуем точку М в системе координат XOУ (рис. 22).

Р а д и у с − в е к т о р точки — это вектор,

который соединяет начало координат с данной точкой.

Если мы знаем радиус-вектор (его модуль r и направление, которое задано углом a), то мы можем найти координаты точки М:

Если мы знаем координаты точки М (х, у), то мы можем найти радиус-вектор:

— модуль радиуса-вектора

— его направление, которое определяет угол a:

— Радиус-вектор и координаты точки х, у — это характеристики положения материальной точки.

1.9. Перемещение

При движении материальной точки ее радиус- вектор и координаты изменяются (рис. 23). За интервал времени Δt радиус-вектор изменяется на величину

Вектор — это перемещение материальной точки (тела) за интервал времени Δ t = t – t ₀.

П е р е м е щ е н и е — это вектор, который соединяет начальное и конечное положения материальной точки на траектории.

Если материальная точка движется криволинейно, то путь S и модуль перемещения Δ r не равны (; S > Δ r; рис. 24, а).

Если материальная точка движется прямолинейно, то путь S и модуль перемещения Δr равны (S = Δ r; рис. 24, б).

Перемещение, так же как и путь, измеряется в единицах длины [Δ r ] = [ S ] = [ ℓ ].

Рис. 24

радиус-вектор	radius-vector	rayon-vecteur	radio-vector
перемещение	displacement	déplacement	desplacimienta

1.10. Скорость

Средняя скорость

С к о р о с т ь — это физическая величина, которая количественно характеризует быстроту движения тела.

Автомобиль движется быстрее человека: скорость автомобиля больше скорости человека.

С р е д н я я с к о р о с т ь — это векторная физическая величина, равная отношению вектора перемещения к интервалу времени, за который это перемещение происходит:

Единица скорости в СИ: [υ] = 1 м/с (один метр в секунду).

Единица скорости в системе СГС: [ υ ] = 1 см/с.

Внесистемная единица скорости: [υ] = 1 км/ч;

На практике мы часто используем понятие средней скорости по пути.

С р е д н я я с к о р о с т ь п о п у т и — это скалярная физическая величина, равная отношению пути к интервалу времени, за который тело проходит этот путь:

М г н о в е н н а я с к о р о с т ь — это скорость, которую имеет тело в данный момент времени (в данной точке траектории).

Чтобы найти мгновенную скорость, надо рас- сматривать перемещение за бесконечно малый интер- вал времени (интервал времени стремится к нулю):

Δ t ® 0

М г н о в е н н а я с к о р о с т ь — это векторная

физическая величина, равная пределу отношения вектора перемещения к интервалу времени Δt, за который это перемещение происходит, когда Δt ® 0:

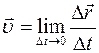Символ lim в формуле обозначает слово «предел».

Вектор мгновенной скорости направлен по прямой линии, касательной к траектории в данной точке (рис. 25).

быстрота	rapidity	rapidité	rapidez
средняя скорость	mean velocity	vitesse moyenne	velocidad media
мгновенная скорость	instant velocity	vitesse instantanée	velocidad instantánea
стремиться к нулю	tend to zero	tendre vers zéro	tender a cero
предел	limit	limite	límite
касательный	tangent	tangente	tangente

1.11. Изменение скорости

Скорость тела не изменяется: = const, если:

— модуль скорости не изменяется: = const;

— направление скорости не изменяется.

Скорость тела изменяется const, если:

— модуль скорости изменяется, или

— направление скорости изменяется, или

— модуль и направление скорости изменяются.

Вектор изменения скорости равен разности векторов скорости и (рис. 26):

(читаем «дельта вэ тау») — это вектор, характеризующий изменение вектора скорости по модулю:

(читаем «дельта вэ эн») — это вектор, характеризующий изменение вектора скорости по направлению.

½ АВ ½ = ½ АD ½ =

, ½ АС ½ =

, ½ DС ½ =

, ½ ВD ½=

Полное изменение вектора скорости равно:

1.12. Ускорение

Ускорение характеризует быстроту изменения скорости.

С р е д н е е у с к о р е н и е — это векторная физическая величина, равная отношению изменения скорости к интервалу времени, за который это изменение происходит:

Вектор среднего ускорения направлен так же, как вектор изменения скорости

Мгновенное ускорение

Единица ускорения в СИ: [ а ] = 1 м/с²(один метр в секунду в квадрате).

Единица ускорения в системе СГС: [ а ] = 1 см/с².

Вектор ускорения имеет два перпендикулярных составляющих: нормальное ускорение и тангенциальное ускорение (рис. 27).

Н о р м а л ь н о е у с к о р е н и е характеризует изменение вектора скорости по направлению

Вектор нормального ускорения всегда направлен перпендикулярно вектору скорости: , .

Если направление вектора скорости не изменяется, то нормальное ускорение равно нулю.

Т а н г е н ц и а л ь н о е у с к о р е н и е характеризует изменение вектора скорости по модулю

Вектор тангенциального ускорения и вектор скорости могут иметь одинаковые или противоположные направления:

— если модуль скорости увеличивается, то вектор тангенциального ускорения и вектор скорости имеют одинаковые направления: − это ускόренное движение (рис. 27);

— если модуль скорости уменьшается, то вектор тангенциального ускорения и вектор скорости имеют противоположные направления − это замéд- ленное движение.