Теорема№3.Признак параллельности прямой и плоскости

Теорема:если прямая вне плоскости параллельна какой либо прямой на плоскости,то эта прямая и плоскость параллельны.

Дано: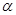

а

b

a|| b

_____________

Доказать:a||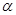

Доказательство.

Применим способ “от противного”.

Предположим,что прямая а не параллельна плоскости и что они пересекаются в точкеK(а =К).Точка К не принадлежит прямой b( К b ) так как прямые a и b параллельны(по условию). Тогда по предыдущей теореме прямые a и b скрещивающиеся,что противоречит условию что а || b.

Значит наше предположение о том,что прямая а пересекает плоскость 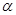- неверно, остается что прямая а параллельна плоскости 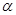.(ч.т.д).