Операции над матрицами

Линейная алгебра

Матрицы

Матрица размера m х n – это прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.

Матрицы принято обозначать заглавными латинскими буквами, а элементы – теми же, но строчными буквами с двойной индексацией.

Например, рассмотрим матрицу А размерности 2 х 3:

В этой матрице две строки (m = 2) и три столбца (n = 3), т.е. она состоит из шести элементов a_ij, где i - номер строки, j - номер столбца. При этом принимает значения от 1 до 2, а от одного до трех (записывается ). А именно, a₁₁= 3; a₁₂= 0; a₁₃= -1; a₂₁= 0; a₂₂= 1,5; a₂₃= 5.

Матрицы А и В одного размера (m х n) называют равными, если они поэлементно совпадают, т.е. a_ij = b_ij для , т.е. для любых i и j (можно записать "i, j).

Матрица-строка – это матрица, состоящая из одной строки, а матрица-столбец – это матрица, состоящая из одного столбца.

Например, - матрица-строка, а .

Квадратная матрица n-го порядка – это матрица, в число строк равно числу столбцов и равно n.

Например, - квадратная матрица второго порядка.

Диагональные элементы матрицы – это элементы, у которых номер строки равен номеру столбца (a_ij, i = j). Эти элементы образуют главную диагональ матрицы. В предыдущем примере главную диагональ образуют элементы a₁₁= 3 и a₂₂= 5.

Диагональная матрица – это квадратная матрица, в которой все недиагональные элементы равны нулю. Например, - диагональная матрица третьего порядка. Если при этом все диагональные элементы равны единице, то матрица называется единичной (обычно обозначаются буквой Е). Например, - единичная матрица третьего порядка.

Матрица называется нулевой, если все ее элементы равны нулю.

Квадратная матрица называется треугольной, если все ее элементы ниже (или выше) главной диагонали равны нулю. Например, 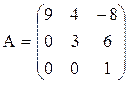- треугольная матрица третьего порядка.

Операции над матрицами

Над матрицами можно производить следующие операции:

1. Умножение матрицы на число. Произведением матрицы А на число l называется матрица В = lА, элементы которой b_ij = la_ij для любых i и j.

Например, если , то .

2. Сложение матриц. Суммой двух матриц А и В одинакового размера m х n называется матрица С = А + В, элементы которой с_ij = a_ij + b_ij для "i, j.

Например, если то

.

Отметим, что через предыдущие операции можно определить вычитание матриц одинакового размера: разность А-В = А + (-1)*В.

3. Умножение матриц. Произведением матрицы А размера m x n на матрицу В размера n x p называется такая матрица С, каждый элемент которой с_ij равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы j-го столбца матрицы В, т.е. .

Например, если

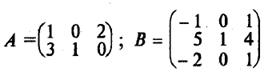, то размер матрицы-произведения будет 2 x 3, и она будет иметь вид:

В этом случае матрица А называется согласованной с матрицей В.

На основе операции умножения для квадратных матриц определена операция возведения в степень. Целой положительной степенью А^m (m > 1) квадратной матрицы А называются произведение m матриц, равных А, т.е.

Подчеркнем, что сложение (вычитание) и умножение матриц определены не для любых двух матриц, а только для удовлетворяющим определенным требованиям к своей размерности. Для нахождения суммы или разности матриц их размер обязательно должен быть одинаковым. Для нахождения произведения матриц число столбцов первой из них должно совпадать с числом строк второй (такие матрицы называют согласованными).

Рассмотрим некоторые свойства рассмотренных операций, аналогичные свойствам операций над числами.

1) Коммутативный (переместительный) закон сложения:

А + В = В + А

2) Ассоциативный (сочетательный) закон сложения:

(А + В) + С = А + (В + С)

3) Дистрибутивный (распределительный) закон умножения относительно сложения:

l(А + В) = lА + lВ

А (В + С) = АВ + АС

(А + В) С = АС + ВС

5) Ассоциативный (сочетательный) закон умножения:

l(АВ) = (lА)В = А(lВ)

A(BС) = (АВ)С

Подчеркнем, что переместительный закон умножения для матриц в общем случае НЕ выполняется, т.е. AB ¹ BA. Более того, из существования AB не обязательно следует существование ВА (матрицы могут быть не согласованными, и тогда их произведение вообще не определено, как в приведенном примере умножения матриц). Но даже если оба произведения существуют, они обычно разные.

В частном случае коммутативным законом обладает произведение любой квадратной матрицы А на единичную матрицу того же порядка, причем это произведение равно А (умножение на единичную матрицу здесь аналогично умножению на единицу при умножении чисел):

АЕ = ЕА = А

В самом деле,

Подчеркнем еще одно отличие умножения матриц от умножения чисел. Произведение чисел может равняться нулю тогда и только тогда, когда хотя бы одно из них равно нулю. О матрицах этого сказать нельзя, т.е. произведение ненулевых матриц может равняться нулевой матрице. Например,

Продолжим рассмотрение операций над матрицами.

4. Транспонирование матрицы представляет собой операцию перехода от матрицы А размера m x n к матрице А^Т размера n x m, в которой строки и столбцы поменялись местами:

%.

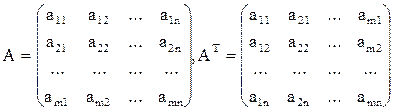Свойства операции транспонирования:

1) Из определения следует, что если матрицу транспонировать дважды, мы вернемся к исходной матрице: (A^T)^T = A.

2) Постоянный множитель можно вынести за знак транспонирования: (lА)^T = lА^T.

3) Транспонирование дистрибутивно относительно умножения и сложения матриц: (AB)^T = B^TA^T и (A + B)^T = B^T + A^T.

Определители матриц

Для каждой квадратной матрицы А вводится число |А|, которое называют ее определителем. Иногда его еще обозначают буквой D.

Это понятие является важным для решения ряда практических задач. Определим его через способ вычисления.

Для матрицы А первого порядка ее определителем называют ее единственный элемент |А| = D₁ = а₁₁.

Для матрицы А второго порядка ее определителем называют число, которое вычисляют по формуле |А| = D₂ = а₁₁* а₂₂ – а₂₁* а₁₂

Для матрицы А третьего порядка ее определителем называют число, которое вычисляют по формуле

Оно представляет алгебраическую сумму, состоящую из 6 слагаемых, в каждое из которых входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Для запоминания формулы определителя принято пользоваться так называемым правилом треугольников или правилом Сарруса (рисунок 6.1).

На рисунке 6.1 схема слева показывает, каким образом выбирать элементы для слагаемых со знаком «плюс», - они находятся на главной диагонали и в вершинах равнобедренных треугольников, основания которых ей параллельны. Схема слева используется для слагаемых со знаком «минус»; на ней вместо главной диагонали берется так называемая побочная.

Определители более высоких порядков вычисляют рекуррентным способом, т.е. определитель четвертого порядка через определитель третьего порядка, определитель пятого порядка через определитель четвертого порядка и т.д. Для описания этого способа необходимо ввести понятия минора и алгебраического дополнения элемента матрицы (сразу же отметим, что сам способ, который будет рассмотрен далее, подходит и для определителей третьего и второго порядка).

Минором М_ij элемента а_ij матрицы n-го порядка называют определитель матрицы (n-1)-го порядка, полученной из матрицы А вычеркиванием i-й строки и j-го столбца.

Каждая матрица n-го порядка имеет n² миноров (n-1)-го порядка.

Алгебраическим дополнением A_ij элемента а_ij матрицы n-го порядка называют его минор, взятый со знаком (-1)^(i+j):

A_ij = (-1)^(i+j)*М_ij

Из определения следует, что A_ij = М_ij, если сумма номеров строки и столбца четная, и A_ij = -М_ij, если она нечетная.

Например, если 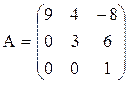, то _; и т.д.

Способ вычисления определителя состоит в следующем: определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

(разложение по элементам i-й строки; );

(разложение по элементам j-го столбца; ).

Например,

Отметим, что и в общем случае определитель треугольной матрицы равен произведению элементов главной диагонали.

Сформулируем основные свойства определителей.

1. Если какая-либо строка или столбец матрицы состоит из одних нулей, то определитель равен 0 (следует из способа расчета).

2. Если все элементы какой-либо строки (столбца) матрицы умножить на одно и то же число, то и ее определитель умножится на это число (также следует из способа расчета – на расчет алгебраических дополнений общий множитель не влияет, а все остальные слагаемые умножены именно на это число).

Замечание: за знак определителя можно выносить общий множитель именно строки или столбца (в отличие от матрицы, за знак которой можно выносить общий множитель всех ее элементов). Например, , но .

3. При транспонировании матрицы ее определитель не изменяется: |А^Т| = |А| (доказательство проводить не будем).

4. При перестановке местами двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

Для доказательства этого свойства вначале предположим, что переставлены две соседние строки матрицы: i-я и (i+1)-я. Для расчета определителя исходной матрицы осуществим разложение по i-й строке, а для определителя новой матрицы (с переставленными строками) – по (i+1)–й (которая в ней такая же, т.е. поэлементно совпадает). Тогда при расчете второго определителя каждое алгебраическое дополнение будет иметь противоположный знак, так как (-1) будет возводиться не в степень (i + j), а в степень (i + 1+ j), а в остальном формулы отличаться не будут. Таким образом, знак определителя изменится на противоположный.

Теперь предположим, что переставлены не соседние, а две произвольные строки, например, i-я и (i+t)-я. Такую перестановку можно представить как последовательное смещение i-й строки на t строк вниз, а (i+t)-й строки - на (t-1) строк вверх[1]. При этом знак определителя поменяется (t + t – 1) = 2t – 1 число раз, т.е. нечетное число раз. Следовательно, в конечном итоге он поменяется на противоположный.

Аналогичные рассуждения можно поменять для столбцов.

5. Если матрица содержит две одинаковые строки (столбца), то ее определитель равен 0.

В самом деле, если одинаковые строки (столбцы) переставить местами, то будет получена та же самая матрица с тем же самым определителей. С другой стороны, по предыдущему свойству он должен поменять знак, т.е. D = -D Û D = 0.

6. Если элементы двух строк (столбцов) матрицы пропорциональны, то определитель равен 0.

Это свойство основано на предыдущем свойстве и выносе за скобку общего множителя (после выноса за скобку коэффициента пропорциональности в матрице будут одинаковые строки или столбцы, и в результате этот коэффициент будет умножаться на ноль).

7. Сумма произведений элементов любой строки (столбца) матрицы на алгебраические дополнения элементов другой строки (столбца) той же матрицы всегда равна 0: 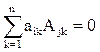при i ¹ j.

Чтобы доказать это свойство, достаточно заменить в матрице А j–ю строку на i–ю. В полученной матрице будет две одинаковые строки, поэтому ее определитель равен 0. С другой стороны, его можно вычислить разложением по элементам j -й строки: .

8. Определитель матрицы не изменяется, если к элементам строки или столбца матрицы прибавить элементы другой строки (столбца), умноженные на одно и тоже число.

В самом деле, пусть к элементам i–й строки прибавляют элементы j-й строки, умноженные на l. Тогда элементы новой i–й строки примут вид
(a_ik + la_jk, "k). Вычислим определитель новой матрицы разложением по элементам i-й строке (отметим, что алгебраические дополнения ее элементов при этом не изменятся):

Мы получили, что этот определитель не отличается от определителя исходной матрицы.

9. Определитель произведения матриц равен произведению их определителей: |АВ| = |А| * |В| (доказательство проводить не будем).

Рассмотренные выше свойства определителей используют для упрощения их вычисления. Обычно стараются преобразовать матрицу к такому виду, чтобы какой-либо столбец или строка содержали как можно больше нулей. После этого определитель легко найти разложением по этой строке или столбцу.

Обратная матрица

Матрицу А^-1 называют обратной по отношению к квадратной матрице А, если при умножении этой матрицы на матрицу А как справа, так и слева получается единичная матрица: А^-1 * А = А * А^-1 = Е.

Из определения следует, что обратная матрица является квадратной матрицей того же порядка, что и матрица А.

Можно отметить, что понятие обратной матрицы аналогично понятию обратного числа (это число, которое при умножении на данное число дает единицу: а*а^-1= а*(1/а) = 1).

Все числа, кроме нуля, имеют обратные числа.

Чтобы решить вопрос о том, имеет ли квадратная матрица обратную, необходимо найти ее определитель. Если определитель матрицы равен нулю, то такая матрица называется вырожденной, или особенной.

Необходимое и достаточное условие существования обратной матрицы: обратная матрица существует и единственна тогда и только тогда, когда исходная матрица невырожденная.

Докажем необходимость. Пусть матрица А имеет обратную матрицу А^-1, т.е. А^-1 * А = Е. Тогда |А^-1 * А| = |А^-1| * |А| = |Е| = 1. Следовательно,
|А| ¹ 0.

Докажем достаточность. Чтобы его доказать, необходимо просто описать способ вычисления обратной матрицы, который мы всегда сможем применить для невырожденной матрицы.

Итак, пусть |А| ¹ 0. Транспонируем матрицу А. Для каждого элемента А^Т найдем алгебраическое дополнение и составим из них матрицу 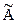, которую называют присоединенной (взаимной, союзной): .

Найдем произведение присоединенной матрицы и исходной . Получим . Таким образом матрица В – диагональная. На ее главной диагонали стоят определители исходной матрицы, а все остальные элементы – нули:

Аналогично можно показать, что .

Если разделить все элементы матрицы на |А|, то будет получена единичная матрица Е.

Таким образом , т.е. .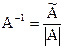

Докажем единственность обратной матрицы. Предположим, что существует другая обратная матрица для А, отличная от А^-1. Обозначим ее X. Тогда А * Х = Е. Умножим слева обе части равенства на А^-1.

А^-1 * А * Х = А^-1 * Е

Е * Х = А^-1

Х = А^-1

Единственность доказана.

Итак, алгоритм вычисления обратной матрицы состоит из следующих шагов:

1. Найти определитель матрицы |А|. Если |А| = 0, то матрица А - вырожденная, и обратную матрицу найти нельзя. Если |А| ¹ 0, то переходят к следующему шагу.

2. Построить транспонированную матрицу А^Т.

3. Найти алгебраические дополнения элементов транспонированной матрицы и построить присоединенную матрицу .

4. Вычислить обратную матрицу, разделив присоединенную матрицу на |А|.

5. Можно проверить правильность вычисления обратной матрицы в соответствии с определением: А^-1 * А = А * А^-1 = Е.

1. Найдем определитель этой матрицы по правилу треугольников:

¹ 0.

Проверку опустим.

Можно доказать следующие свойства обращения матриц:

1) |А^-1| = 1/|А|

2) (А^-1)^-1 = А

3) (А^m)^-1 = (А^-1)^m

4) (АB)^-1 = B^-1 * А^-1

5) (А^-1)^T = (А^T)^-1

Ранг матрицы

Минором k-го порядка матрицы А размера m х n называют определитель квадратной матрицы k-го порядка, которая получена из матрицы А вычеркиванием каких-либо строк и столбцов.

Из определения следует, что порядок минора не превосходит меньшего из ее размеров, т.е. k £ min {m; n}. Например, из матрицы А_5х3 можно получить квадратные подматрицы первого, второго и третьего порядков (соответственно, рассчитать миноры этих порядков).

Рангом матрицы называют наивысший порядок отличных от нуля миноров этой матрицы (обозначают rang А, или r(А)).

Из определения следует, что

1) ранг матрицы не превосходит меньшего из ее размеров, т.е.
r(А) £ min {m; n};

2) r(А) = 0 тогда и только тогда, когда матрица нулевая (все элементы матрицы равны нулю), т.е. r(А) = 0 Û А = 0;

3) для квадратной матрицы n-го порядка r(А) = n тогда и только тогда, когда эта матрица А невырожденная, т.е. r(А) = n Û |А| ¹ 0.

На самом деле, для этого достаточно вычислить только один такой минор (тот, который получен вычеркиванием третьего столбца (потому что в остальных будет присутствовать нулевой третий столбец, и поэтому они равны нулю).

По правилу треугольника = 1*2*(-3) + 3*1*2 + 3*(-1)*4 – 4*2*2 – 1*(-1)*1 – 3*3*(-3) = -6 +6 – 12 – 16 + 1 +27 = 0.

Поскольку все миноры третьего порядка нулевые, r(А) £ 2. Так как существует ненулевой минор второго порядка, например,

Очевидно, что использованные нами приемы (рассмотрение всевозможных миноров) не подходят для определения ранга в более сложных случаях ввиду большой трудоемкости. Обычно для нахождения ранга матрицы используют некоторые преобразования, которые называют элементарными:

1). Отбрасывание нулевых строк (столбцов).

2). Умножение всех элементов строки или столбца матрицы на число, отличное от нуля.

3). Изменение порядка строк (столбцов) матрицы.

4). Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

5). Транспонирование.

Если матрица А получена из матрицы B элементарными преобразованиями, то эти матрицы называют эквивалентными и обозначают А ~ В.

Теорема. Элементарные преобразования матрицы не изменяют ее ранг.

Доказательство теоремы следует из свойств определителя матрицы. В самом деле, при этих преобразованиях определители квадратных матриц либо сохраняются, либо умножаются на число, не равное нулю. В результате наивысший порядок отличных от нуля миноров исходной матрицы остается прежним, т.е. ее ранг не меняются.

С помощью элементарных преобразований матрицу приводят к так называемому ступенчатому виду (преобразуют в ступенчатую матрицу), т.е. добиваются, чтобы в эквивалентной матрице под главной диагональю стояли только нулевые элементы, а на главной диагонали – ненулевые:

Ранг ступенчатой матрицы равен r, так как вычеркиванием из нее столбцов, начиная с (r + 1)-го и дальше можно получить треугольную матрицу r-го порядка, определитель которой будет отличен от нуля, так как будет представлять собой произведение ненулевых элементов (следовательно, имеется минор r-го порядка, не равный нулю):

Пример. Найти ранг матрицы

1). Если а₁₁ = 0 (как в нашем случае), то перестановкой строк или столбцов добьемся того, чтобы а₁₁ ¹ 0. Здесь поменяем местами 1-ю и 2-ю строки матрицы:

2). Теперь а₁₁ ¹ 0. Элементарными преобразованиями добьемся того, чтобы все остальные элементы в первом столбце равнялись нулю. Во второй строке a₂₁ = 0. В третьей строке a₃₁ = -4. Чтобы вместо (-4) стоял 0, прибавим к третьей строке первую строку, умноженную на 2 (т.е. на (-а₃₁/а₁₁) = -(-4)/2 =
= 2). Аналогично к четвертой строке прибавим первую строку (умноженную на единицу, т.е. на (-а₄₁/а₁₁) = -(-2)/2 = 1).

3). В полученной матрице а₂₂ ¹ 0 (если бы было а₂₂ = 0, то можно было бы снова переставить строки). Добьемся, чтобы ниже диагонали во втором столбце тоже стояли нули. Для этого к 3-й и 4-й строкам прибавим вторую строку, умноженную на -3 ((-а₃₂/а₂₂) = (-а₄₂/а₂₂) = -(-3)/(-1) = -3):

4). В полученной матрице две последние строки – нулевые, и их можно отбросить:

Получена ступенчатая матрица, состоящая из двух строк. Следовательно, r(A) = 2.