Рассмотрим квадратную матрицу A n -го порядка.
Выберем i, j -ый элемент этой матрицы и вычеркнем i -ую строку и j -ый столбец. В результате мы получаем матрицу (n – 1)-го порядка, определитель которой называется минором элемента и обозначается символом Mi j:
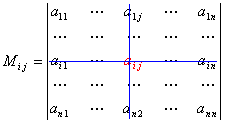
Алгебраическое дополнение Ai , j элемента ai j определяется формулой 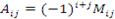
Теорема о разложении определителя по элементам строки. Определитель матрицы A равен сумме произведений элементов строки на их алгебраические дополнения: 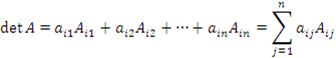
Теорема о разложении определителя по элементам столбца. Определитель матрицы A равен сумме произведений элементов столбца на их алгебраические дополнения: 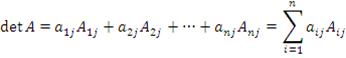
 2015-01-30
2015-01-30 2874
2874
