Линейные уравнения второго порядка

1. Основные понятия.

Линейными дифференциальными уравнениями второго порядка называются уравнения вида

(I)

функции , , 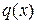непрерывны в некотором промежутке .

Уравнение (I) называется линейным неоднородным или уравнением с правой частью, если . Если , то уравнение называется линейным однородным.

Однородное уравнение с той же левой частью, что и данное неоднородное, называется соответствующим ему.

Теорема 1. Общее решение линейного неоднородного уравнения складывается из общего решения соответствующего ему однородного уравнения и частного решения 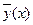неоднородного:

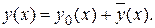
Ограничимся рассмотрением линейных уравнений с постоянными коэффициентами, которые широко используются в механике, электротехнике.

2. Линейное однородное уравнение с постоянными коэффициентами имеет вид: , (II)

где – вещественные числа.

Характеристическим уравнением называется уравнение , его корни и . Характеристическое уравнение получают заменой в данном линейном однородном уравнении.

Теорема 2. 1) Если корни характеристического уравнения вещественные различные и , то общее решение однородного уравнения

, (II.I)

2) если = = , то

, (II.II)

3) если корни комлексно-сопряженные то

(II.III)

Пример 1. Найти общее решение .

Решение. Составим характеристическое уравнение ; ; , по (II.I) имеем .

Пример 2. Найти частное решение уравнения , если ; .

Решение. По (II.II) общее решение Выбираем и 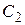так, чтобы выполнялись начальные условия: ; ; ; ; . Подставив найденные и 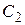в общее решение, получим искомое частное решение: .

Пример 3. Найти общее решение .

Решение. ; по (II.III) имеем общее решение:

Пример 4. Найти общее решение уравнения гармонических колебаний .

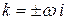
Решение. 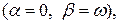по (II.III) общее решение

3. Линейные неоднородные уравнения с постоянными коэффициентами . Подбор частного решения методом неопределенных коэффициентов

Этот метод, наиболее важный для приложений, применим только в том случае, когда правая часть уравнения имеет вид квазиполинома:

где и – действительные числа, и – многочлены степеней и .

Теорема 3. Частное решение линейного неоднородного дифференциального уравнения следует искать в виде

1) если то (II.IV)

где – многочлены с неопределенными коэффициентами степени , записываются так: и т.д. Чтобы найти неопределенные коэффициенты, нужно частное решение подставить в заданное уравнение.

2) если то (II.V)

Коэффициенты и находят аналогично коэффициентам 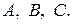Если в функцию входит только или , в частное решение надо включать оба слагаемых.

На основании теоремы 1 общее решение неоднородного уравнения складывается из общего решения однородного (теорема 2) и частного неоднородного (теорема 3).

Пример 1. Найти общее решение дифференциального уравнения

Решение. Общее решение данного уравнения имеет вид где – общее решение соответствующего однородного уравнения а – частное решение данного неоднородного уравнения. Решая характеристическое уравнение , найдем его корни: . По формуле (II.II):

Найдем частное решение неоднородного уравнения с правой частью: По формуле (II.IV) коэффициенты А и В подлежат определению из условия, что решение данного уравнения. Находим производные:

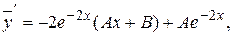
подстановка , и в уравнение дает (после сокращения на ):

т.е. Для того, чтобы равенство было верным, достаточно совпадения коэффициентов при одних и тех же степенях 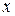в обеих частях равенства:

Из этих уравнений находим А= 1, В= 2. Следовательно, функция является частным решением данного уравнения, а функция

его общим решением.

Пример 2. Найти общее решение уравнения: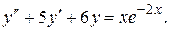

Решение. Характеристическое уравнение: 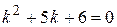. Его корни: По формуле (II.I): .

Вид правой части здесь такой же, как в примере 5, но поэтому Следовательно,

Подстановка в уравнение, сокращение на дает: , ; , . Тогда:

Общее решение данного уравнения :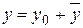

Пример 3. Найти общее решение уравнения .

Решение. Характеристическое уравнение: Его корни: Общее решение однородного уравнения: Правая часть исходного уравнения: Частное решение найдем по формуле (II.IV):

Подставим в исходное уравнение: . Тогда .

Пример 4. Найти общее решение дифференциального уравнения

Решение. Характеристическое уравнение имеет корни . По формуле (II.III):

по формуле (II.V):

Подстановка в дифференциальное уравнение дает: 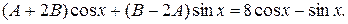Для того чтобы это равенство выполнялось, достаточно совпадения коэффициентов при в обеих частях равенства:

Решая систему, получим Тогда частное решение неоднородного уравнения: и общее решение данного уравнения