2015-10-22
2121
Пользуясь приближенным значением числа, нужно иметь возможность судить о степени его точности. С этой целью вычисляют его абсолютную и относительную погрешности.
Абсолютная погрешность 
приближенного числа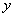 
равна абсолютной величине разности между точным числом 
и его приближенным значением:
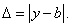(12)
Относительной погрешностью 
приближенного числа 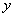называется отношение абсолютной погрешности этого числа к абсолютной величине соответствующего точного числа:
(13)
Если точное число неизвестно, то
(14)
Иногда, прежде чем применить формулу (11), требуется предварительно преобразовать исходную величину. Как правило, это делается в двух целях. Во-первых, надо добиться, чтобы величина 
была достаточно малой по сравнению с 
, так как чем меньше 
, тем точнее результат приближенного вычисления. Во-вторых, желательно, чтобы величина 
вычислялась просто.
Пример 4. Пользуясь понятием дифференциала, вычислить приближенно 
. Оценить точность полученного результата.
Решение. Рассмотрим функцию
Её производная равна
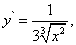
а формула (11) примет вид
В данном случае было бы нерационально вычислять приближенно следующим образом:
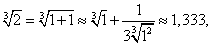
так как значение
не является малым по сравнению со значением производной в точке
Здесь удобно предварительно вынести из под корня некоторое число, например 4/3. Тогда
Теперь, полагая
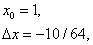
получим
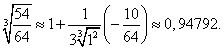
Умножая на 4/3, находим
Принимая табличное значение корня
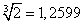
за точное число, оценим по формулам (12) и (13) абсолютную и относительную погрешности приближенного значения:
