Дифференциал функции в точке x и обозначают
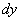
или
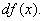
Следовательно,
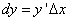 (1)
(1)
или
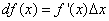 , (2)
, (2)
поскольку дифференциал функции y = f (x) равен произведению её производной на приращение независимой переменной.
Замечание. Нужно помнить, что если x – исходное значение аргумента, а 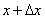 - наращенное значение, то производная в выражении дифференциала берётся в исходной точке x; в формуле (1) этого не видно из записи.
- наращенное значение, то производная в выражении дифференциала берётся в исходной точке x; в формуле (1) этого не видно из записи.
Дифференциал функции можно записать в другой форме:
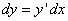 (3)
(3)
или
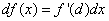 (4)
(4)
Пример 1. Найти дифференциалы функций:
1) 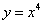 ;
;
2) 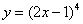 ;
;
3) 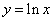 ;
;
4) 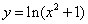 .
.
Решение. Применяя формулы дифференцирования степенной и логарифмической функций из таблицы производных, а также формулу (4), находим:
1) 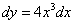 ;
;
2) 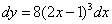 ;
;
3) 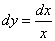 ;
;
4) 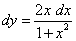 .
.
 2015-10-22
2015-10-22 1104
1104
