IV. Найти проекцию 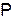 точки
точки 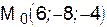 на плоскость
на плоскость 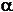 , проходящую через прямую
, проходящую через прямую 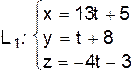 параллельно прямой
параллельно прямой 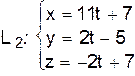 .
.
V. 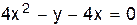 .
.
VI. 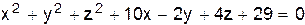 .
.
VII. 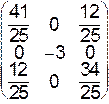 .
.
Вариант №12
I. 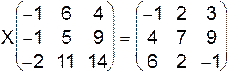 .
.
II.а. 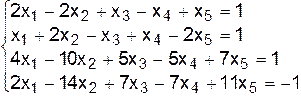 .
.
II.б. 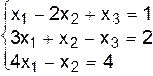 .
.
III. Даныточки: 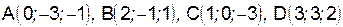 . Вычислить:
. Вычислить:
а. Единичный вектор, коллинеарный и противоположно направленный вектору 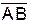 .
.
б. Синус угла между векторами 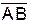 и
и 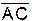 .
.
с. Будут ли вектора 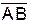 ,
, 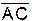 и
и 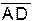 компланарны.
компланарны.
IV. Плоскость 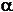 проходит через точку
проходит через точку 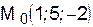 и прямую
и прямую 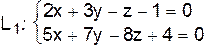 . Прямая
. Прямая 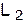 проходит через точку
проходит через точку 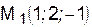 перпендикулярно двум прямым
перпендикулярно двум прямым 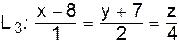 и
и 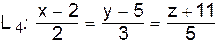 . Найти точку
. Найти точку 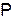 пересечения плоскости
пересечения плоскости 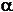 и прямой
и прямой 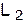 .
.
V. 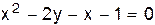 .
.
VI. 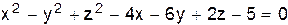 .
.
VII. 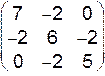 .
.
Вариант №13
I. 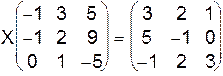 .
.
II.а. 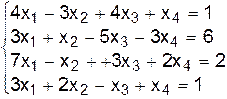 .
.
II.б. 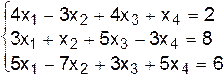 .
.
III. На векторах 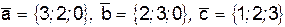 построен параллелепипед. Вычислить:
построен параллелепипед. Вычислить:
а. Проекцию вектора 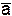 на направление вектора
на направление вектора 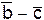 .
.
б. Площадь грани, образованной векторами 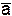 и
и 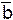 .
.
с. Высоту параллелепипеда, опущенную на грань 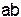 .
.
IV. Написать уравнение плоскости 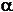 , проходящей через прямую
, проходящей через прямую 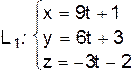 параллельно прямой
параллельно прямой 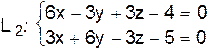 .
.
V. 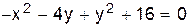 .
.
VI. 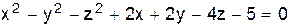 .
.
VII. 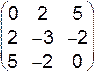 .
.
Вариант №14
I. 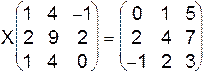 .
.
II.а. 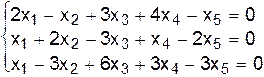 .
.
II.б. 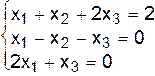 .
.
III. На векторах 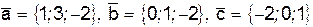 построен параллелепипед. Вычислить:
построен параллелепипед. Вычислить:
а. Косинус угла между векторами 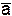 и
и 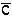 .
.
б. Высоту параллелограмма, построенного на векторах 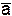 и
и 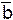 .
.
с. Будут ли вектора 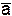 ,
, 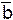 ,
, 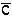 компланарны.
компланарны.
IV. Плоскост 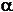 проходит через точку
проходит через точку 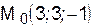 параллельно прямым
параллельно прямым 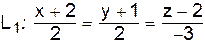 и
и 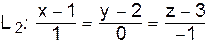 . Найти точку
. Найти точку 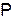 , симметричную точке
, симметричную точке 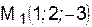 относительно плоскости
относительно плоскости 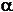 .
.
V. 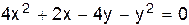 .
.
VI. 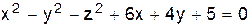 .
.
VII. 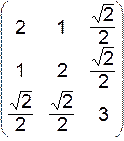 .
.
Вариант №15
I. 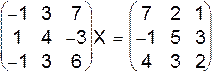 .
.
II.а. 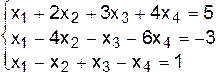 .
.
II.б. 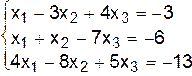 .
.
III. Даны точки: 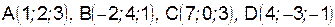 . На векторах
. На векторах 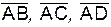 построена пирамида. Вычислить:
построена пирамида. Вычислить:
а. Направляющие косинусы вектора 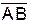 .
.
б. Площадь треугольника  .
.
С. Объем пирамиды.
IV. Написать уравнение плоскости 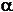 , проходящей через прямую
, проходящей через прямую 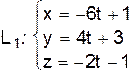 параллельно прямой
параллельно прямой 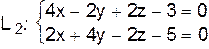 .
.
V. 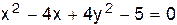 .
.
VI. 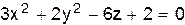
VII. 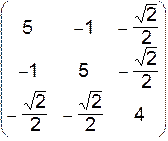 .
.
Вариант №16
I. 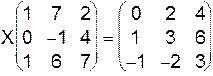 .
.
II.а. 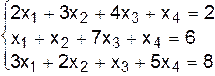 .
.
II.б. 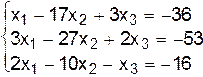 .
.
III. На векторах 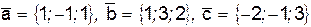 построен параллелепипед. Вычислить:
построен параллелепипед. Вычислить:
а. Проекцию вектора 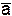 на направление, противоположное направлению вектора
на направление, противоположное направлению вектора 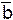 .
.
б. Высоту параллелепипеда, опущенную на грань 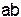 .
.
 2015-10-22
2015-10-22 516
516








