2015-10-22
4625
Теорема о проецировании прямого угла:
Если одна сторона прямого угла параллельна плоскости проекций, а другая ей не перпендикулярна, то прямой угол проецируется на эту плоскость проекций без искажения.
Если на чертеже есть изображение прямого угла, то одна из его сторон обязательно натуральная величина
8. Плоскость. Способы задания плоскости на чертежах. Следы плоскости. Принадлежность прямой и плоскости, точки и плоскости.
На комплексном чертеже плоскость S можно задать: 1) проекциями трех точек, не лежащих на одной прямой; 2) проекциями прямой и точки, взятой вне этой прямой; 3) проекциями двух пересекающихся прямых; 4) проекциями двух параллельных прямых;
5) проекциями плоской фигурой; 6) следами плоскости. Все способы позволяют выделить из множества точек пространства точки, принадлежащие данной плоскости. Способ задания плоскости указывают в круглых скобках
След плоскости – это линия ее пересечения с соответствующей плоскостью проекций.
Принадлежность прямой плоскости
|
|
|
Прямая принадлежит плоскости, если она проходит:
1) через две точки этой плоскости;
2) через одну точку плоскости и параллельно какой-нибудь прямой, лежащей в этой плоскости
Принадлежность точки плоскости
Точка будет лежать в плоскости, если она принадлежит какой-либо прямой этой плоскости. Воспользуемся этим положением:
1) при чтении чертежа;
2) при построении точки, лежащей в данной плоскости
Если плоскость занимает проецирующее положение, то соответствующие проекции всех точек и прямых данной плоскости совпадают с ее следом.
Это собирательное свойство проецирующих плоскостей
9. Плоскости общего и частного положения. Свойства проекций проецирующих плоскостей. Плоскости уровня и свойства их проекций. Главные линии в плоскостях общего и частного положения.
Положение плоскости относительно плоскостей проекций
Плоскость общего положения наклонена ко всем плоскостям проекций
Плоскость частного положения перпендикулярна или параллельна одной из плоскостей проекций
Плоскость, перпендикулярная одной из плоскостей проекций, называется проецирующей плоскостью:
Горизонтально проецирующая плоскость ^ П1
Фронтально проецирующая плоскость ^ П2 Профильно-проецирующая плоскость ^ П3
Плоскость, параллельная плоскости проекций, называется плоскостью уровня (дважды проецирующей):
Горизонтальная плоскость êê П1
Фронтальная плоскость êê П2
Профильная плоскость êêП3
Главные линии плоскости
Горизонталей плоскости бесчисленной множество,
все они параллельны между собой
Горизонтальный след – это горизонталь нулевого уровня
|
|
|
Горизонталь плоскости – это прямая, лежащая в плоскости и параллельная горизонтальной плоскости проекций. Фронтальная проекция горизонтали параллельна оси x. Положение горизонтали в плоскости определяют две точки (например, В и 1)
Фронталей плоскости бесчисленное множество, все они параллельны между собой.
Фронтальный след – это фронталь нулевого уровня.
Фронталь плоскости – это прямая, лежащая в плоскости и параллельная фронтальной плоскости проекций.
Горизонтальная проекция фронтали параллельна оси x. Положение фронтали в плоскости определяют две точки (например, В и 2)
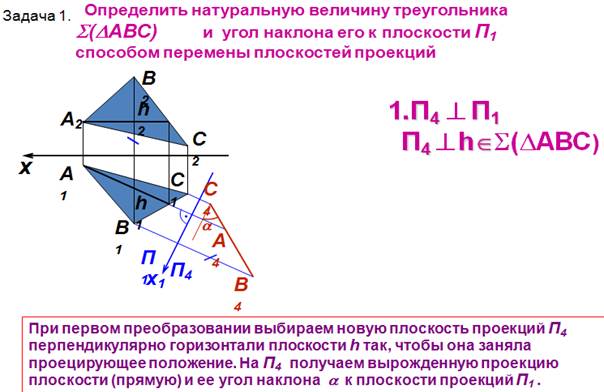
10. Определение натуральной величины плоскости и углов наклона ее к плоскостям проекций способом перемены плоскостей проекций.
11 Взаимное положение прямой и плоскости: прямая, параллельная плоскости.
Прямая параллельна плоскости: общих точек нет
Признак параллельности:
Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости
Если прямая а параллельна плоскости общего положения, то в плоскости строят вспомогательную прямую n и выполняют условие параллельности одноименных проекций прямых а и n. Если плоскость проецирующая, то одна из проекций искомой прямой m параллельна следу плоскости
Взаимное положение прямой и плоскости: прямая, пересекающая плоскость. Алгоритм определения точки пересечения прямой и плоскости частного и общего положения. Определение видимости прямой с помощью конкурирующих точек.
Пересечение прямой общего положения с плоскостью общего положения:
Алгоритм:
- Через данную прямую m проводят вспомогательную плоскость Q.
- Находят линию пересечения 1-2 плоскостей: заданной S и вспомогательной Q. 3. На полученной линии пресечения 1-2 находят общую точку К с заданной прямой m. 4. Определяют видимость прямой m
