Поведение случайных величин, которые составляют заданный гидрологический ряд наблюдений, можно охарактеризовать тремя параметрами:
- средним арифметическим значением;
- коэффициентом вариации;
- коэффициентом асимметрии.
Среднее арифметическое значение ряда:
 (2)
(2)
где: Qi – максимальный расход весеннего половодья, м3/с;
n – количество членов ряда.
Коэффициенты вариации и асимметрии определяются в соответствии с СП 33-101-2003 тремя методами: моментов, наибольшего правдоподобия и графоаналитическим.
1. Метод моментов. Коэффициент вариации Сv характеризует меру изменчивости членов ряда относительно среднего арифметического значения и определяется по формуле (при Сv < 0.6):
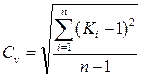 , (3)
, (3)
где Ki – частное от деления i -го члена ряда на среднее арифметическое этого ряда, т.е.  .
.
Коэффициент асимметрии Сs характеризует отличие по величине и количеству положительных (больше средних) и отрицательных (меньше средних) отклонений от среднего арифметического значения ряда. Для симметричных рядов (нормальное распределение ежегодных вероятностей превышения значений ряда) эти отклонения повторяются одинаково часто, поэтому Cs = 0. Для несимметричных рядов Cs ≠ 0, а коэффициент асимметрии определяется по формуле (при Сs < 1,0):
 (4)
(4)
Расчеты по определению статистических характеристик сводятся в табл. 3. В верхней строке этой таблицы указана точность, с которой необходимо определить соответствующие величины.
Для проверки правильности определения среднего значения сравниваем суммы положительных и отрицательных значений ∑(Ki - 1). Они должны отличаться один от другого не более чем на 5%.
2. Метод наибольшего правдоподобия. Для оценки коэффициентов вариации и асимметрии этим методом необходимо предварительно определить величины статистик:
 (5)
(5)

Результаты расчета, необходимые для определения этих статистик, сводятся в табл. 3. По рассчитанным значениям статистик по одной из номограмм (прил. 4) определяют характеристики ряда: Cv, Cs/Cv и Cs.
3. После определения параметров статистического ряда этими методами, по таблицам прил. 4 находятся ординаты (модульные коэффициенты) теоретической (аналитической) кривой трехпараметрического гамма-распределения ежегодных вероятностей превышения значений гидрологической характеристики или кривой обеспеченности. По ним вычисляем максимальные расходы воды заданной обеспеченности Qр% = Кр% * Q ср (табл. 4).
4. В задаче требуется построить эмпирическую и теоретические кривые обеспеченности.
Эмпирическую обеспеченность или ежегодную вероятность превышения гидрологических характеристик определяют по формуле:
 , % (6)
, % (6)
где m – порядковый номер члена ряда, выстроенного в убывающем порядке (табл. 3).
Результаты расчета эмпирической обеспеченности приведены в табл. 3.
5. На клетчатках вероятности (рис. 4 или прил. 3) по данным табл.3 и 4строим:
- эмпирическую кривую обеспеченности;
- теоретическую кривую обеспеченности (метод моментов);
- теоретическую кривую обеспеченности (метод наибольшего правдоподобия).
6. Графоаналитический метод определения параметров биномиальной кривой обеспеченности (при надлежащем обосновании возможности её применения) допускается использовать на ранних стадиях проектирования гидротехнических сооружений.
Для этого по эмпирической кривой обеспеченности, построенной на клетчатках вероятности (рис. 4 или прил.3) определяется коэффициент скошенности:
S = (Q 5 + Q 95 - 2 Q 50) / (Q 5 - Q 95), (7)
где Q 5%, Q 50% и Q 95% - величины расходов воды 5, 50 и 95% обеспеченности, устанавливаемые по эмпирической кривой (рис. 4 или прил. 3).
Коэффициент асимметрии находим по прил.4 в зависимости от величины коэффициента скошенности S. Из этого приложения также выписываются значения коэффициентов Фостера: Ф50% и (Ф5% - Ф95%).
Среднее квадратическое отклонение будет равно:
σ ' = (Q 5 - Q 95) / (Ф5 - Ф95) (8)
Уточненное значение средней величины ряда определим по формуле:
Q ср’ = Q 50% - Ф50% * σ ’ (9)
Тогда коэффициент вариации:
Cv’ = σ’ / Q ср’. (10)
Модульный коэффициент р% обеспеченности будет равен:
Кр% = Фр% * Сv’ + 1,(11)
где Фр% - коэффициент Фостера, определяемый по прил. 4 в зависимости от коэффициента асимметрии Cs и обеспеченности р %.
Искомый максимальный расход воды 1% обеспеченности равен:
Q 1% = K 1% * Q ср’ (12)
Пример
Исходные данные:
Ряд наблюдений за максимальным расходом воды в реке А продолжительностью n =31 год для выбранного варианта (см. прил. 1).
1. Вычислим статистические характеристики ряда наблюдений, предварительно выполнив расчеты по форме табл.3
 = 11378 / 31 = 367 м3/с.
= 11378 / 31 = 367 м3/с.
+ ∑ (Кi - 1) = 3.26
- ∑ (Ki - 1) = - 3.25
Суммы положительных и отрицательных значений ∑(Ki – 1) отличаются менее чем на 5%.
а) метод моментов:

 = 0.26
= 0.26
 =
=  = 0.059
= 0.059
б) метод наибольшего правдоподобия:

 = - 0,016
= - 0,016
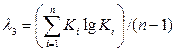
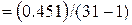 = 0,015
= 0,015
По номограмме (прил. 4) определим:
Cv = 0.26, Cs / Cv = 0.4, Cs = (Cs/Cv) * Cv = 0.4 * 0.26 = 0.1
2. По таблицам прил. 4 определим ординаты теоретических кривых обеспеченности и величины максимальных расходов воды разной вероятности превышения (табл. 4). При Cs / Cv < 0.5 для определения ординат кривых обеспеченности используется таблица прил. 4 при Cs / Cv = 0.5.
Таблица 3
| m | Qi в убывав. порядке | Ki | Ki -1 | (Ki -1)2 | (Ki -1)3 | p, % | lg Ki | Ki *lg Ki |
| Точность | 0,01 | 0,01 | 0,001 | 0,0001 | 0,1 | 0,001 | 0,001 | |
| … … | …. … | 1,57 1,43 … … 0,54 0,50 | 0,57 0,43 … … -0,46 -0,50 | 0,325 0,185 … … 0,212 0,250 | 0,1852 0,0795 … … -0,0973 -0,1250 | 3,1 6,3 … … 93,8 96,9 | 0,196 0,155 … … -0,268 -0,301 | 0,308 0,222 … … -0,145 -0,150 |
| ∑ Qi = =11378 | + 3.26 - 3.25 | ∑ = =2.028 | ∑= =+0.0291 | ∑= = -0.475 | ∑= =0.451 |
Таблица 4
Ординаты теоретической кривой обеспеченности
максимальных расходов воды
а) метод моментов (Q ср = 367 м3/с, Cv = 0,26, Cs = 0,059)
| p, % | 0,1 | |||||||
| Кр % | 1,80 | 1,60 | 1,41 | 1,32 | 1,16 | 1,0 | 0,83 | 0,59 |
| Qр %, м3/с |
б) метод наибольшего правдоподобия (Q ср = 367 м3/с, Cv = 0.26, Cs = 0,1)
| p,% | 0,1 | |||||||
| Кр% | 1,80 | 1,60 | 1,42 | 1,33 | 1,17 | 0,99 | 0,84 | 0,60 |
| Qр%, м3/с |
3. На клетчатках вероятности (рис.4 или прил.3) по данным табл.3 и 4 строим (рис. 4):
- эмпирическую кривую обеспеченности;
- теоретическую кривую обеспеченности (метод моментов);
- теоретическую кривую обеспеченности (метод наибольшего правдоподобия).
4. Для определения Q 1% графоаналитическим методом, используя построенную эмпирическую кривую обеспеченности (рис.4), устанавливаем величины расходов воды с вероятностью превышения 5, 50 и 95%:
Q 5% = 542 м3/с, Q 50% = 365 м3/с, Q 95% = 200 м3/с.
Коэффициент скошенности:
S = (Q 5% + Q 95% - 2 * Q 50%) / (Q 5% - Q 95%) =
= (542 + 200 – 2 * 365) / (542 – 200) = 0,035.
Коэффициент асимметрии и другие параметры определим по прил. 4: Cs = 0,11, Ф50% = -0,022, Ф5% - Ф95% = 3,28.
|

Рис.4. Кривые обеспеченности: (1 – эмпирическая, 2 – метод моментов, 3 – метод наибольшего правдоподобия).
Среднее квадратическое отклонение равно:
σ’ = (Q 5% - Q 95%) / (Ф5% - Ф95%) =
= (542 – 200) / 3,28 = 104,3 м3/с.
Уточненное значение средней арифметической величины найдем по формуле: Q ср’ = Q 50% - Ф50% * σ’ = 365 + 0,022 * 104,3 = 367,3 м3/с.
Тогда, коэффициент вариации:
Cv’ = σ’ / Q ср’ = 104,3 / 367,3 = 0,28.
Расчетный модульный коэффициент при р = 1% равен:
К 1% = Ф1% * Сv’ + 1,
где Ф1% - коэффициент Фостера, определяемый по прил. 4 в зависимости от коэффициента асимметрии Cs = 0,11 и обеспеченности р = 1%. Ф1% = 2,40.
К 1% = 2,40 * 0,28 + 1 =1,67.
Максимальный расход воды 1% обеспеченности, определенный графоаналитическим методом, равен:
Q 1% = K 1% * Q ср’ = 1,67 * 367,3 = 613,4 м3/с.
5. В качестве расчетного максимального расхода воды 1% обеспеченности принимаем большее из значений, определенных методами моментов и наибольшего правдоподобия, т.е. Q 1% = 587 м3/c.
На ранних стадиях проектирования за расчетный максимальный расход воды 1% обеспеченности допускается принимать его значение, полученное графоаналитическим методом при условии обоснования возможности применения биномиальной кривой обеспеченности, т.е. Q 1% = 613,4 м3/c.
Задача 3 (МТ, ВиВ)
 2015-10-22
2015-10-22 1348
1348








