Задача о выборе средства доставки груза

Пусть через обозначены грузообразующие пункты с объемами груза в них 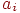. Имеется средств доставки груза (видов транспорта); грузоподъемность - го средства доставки составляет , а наличный его парк равен . Грузы подлежат доставке в один центральный пункт (склад); затраты при осуществлении одной единицей средства доставки рейса от пункта до склада равны . Требуется составить наиболее экономный план доставки.

Через обозначим количество средств доставки типа , отправляющееся из пункта . Тогда задача сведется к минимизации целевой функции вида (7.1.) при условиях (7.2.) и

(7.5)

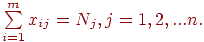
(7.6)

Распределительная задача имеет весьма разнообразные приложения. Большое число практических ее интерпретаций можно найти в монографии Д.Б. Юдина и Е.Г. Гольштейна (Юдин Д.Б., Гольштейн Е.Г., Задачи и методы линейного программирования. Изд. 2-е переработанное и дополненное, М., "Советское радио", 1964.)