 Рис. 28. Параллелепипед Рис. 28. Параллелепипед | Рассмотрим охлаждение параллелепипеда в среде с постоянной температурой и с постоянным коэффициентом теплоотдачи 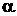 на всех гранях (рис. 28). В начальный момент времени температура во всех точках параллелепипеда одинакова и равна на всех гранях (рис. 28). В начальный момент времени температура во всех точках параллелепипеда одинакова и равна  . Размеры параллелепипеда равны . Размеры параллелепипеда равны 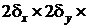 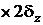 . Начало координат поместим в центр параллелепипеда. Уравнение теплопроводности имеет вид . Начало координат поместим в центр параллелепипеда. Уравнение теплопроводности имеет вид  . . |
Параллелепипед можно рассматривать как тело, образованное пересечением трёх бесконечных пластин толщиной  . В таком теле при принятых условиях температурное поле симметрично относительно центра параллелепипеда. Решение данной задачи может быть получено на основании теоремы перемножения решений. Решение представляется в виде
. В таком теле при принятых условиях температурное поле симметрично относительно центра параллелепипеда. Решение данной задачи может быть получено на основании теоремы перемножения решений. Решение представляется в виде
 ,
,
где  ;
;  ;
;  есть решения одномерных уравнений теплопроводности для трёх бесконечных пластин
есть решения одномерных уравнений теплопроводности для трёх бесконечных пластин  , а
, а
 .
.
 2017-11-30
2017-11-30 1022
1022








