Координатные уравнения плоскости

• Общее уравнение плоскости: Ax+By+Cz+D=0; n(A;B;C); A²+B²+C²>0
докажем, что плоскость имеет вид: Ax+By+Cz+D=0; выберим на плоскости М₁(х₁;у₁;z₁), М₂(х₂;у₂;z₂), М₃(х₃;у₃;z₃); вектора М₁М(х-х₁;у-у₁;z-z₁), М₁М₂(х₂-х₁;у₂-у₁;z₂-z₁) ̴ (a_x;a_y;a_z), М₁М₃(х₃-х₁;у₃-у₁;z₃-z₁) ̴ (b_x;b_y;b_z). Точка М₁ тогда и только тогда будет принадлежать (ϵ) плоскости, если векторы компланарны:
М₁М•М₁М₂•М₁М₃= 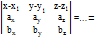A(х-х₁)+B(у-у₁)+C(z-z₁)=0
• Уравнение плоскости проходит через точку перпенд. (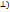 заданному вектору:

ур-ие плоск. проходящей через 3 точки

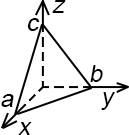• Уравнение плоскости в отрезках на осях: Ax+By+Cz=-D → →

• Расстояние от точки до плоскости. пример: найти расстояние от Мо(2;-1.7) до плоскости 3x-4y-22z+5=0. Мо(xoyo;zo); Ax+By+Cz+D=0

• Нормальное уравнение плоскости.
ОК (Q); OK=p; M(x;y;z); α,β,γ – углы, обр. единым вектором е
с осями Ох, Оу, Oz. Тогда е=(cos α;cos β; cos γ), r = OM=(x;y;z)
При любом положении точки М на плоск. Q проекция радиус-
вектора r на направление вектора e всегда равно p: пр _еr=p
r•e-p=0 - нормальное уравнение плоскости в векторном виде
x•cosα + y•cosβ + z•cosγ – p = 0 нормальное уравнение плоскости в координатном виде