Понятие множества является одним из основных неопределяемых понятий математики. Под множеством понимают совокупность (собрание, класс, семейство...) некоторых объектов, объединенных по какому-либо признаку. Объекты, из которых состоит множество, называются его элементами.  , где x-элемент множества.
, где x-элемент множества.
1.Объединением (или суммой) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств. 
2. Пересечением (или произведением) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит множеству А и множеству В.

3.Разностью множеств А и В называется множество С, состоящее из всех элементов множества А, которые не принадлежат множеству В. 
4. 
Множество X называется ограниченным сверху(снизу), если существует такое число С, что для любого  выполняется неравенство x ≤ C (x ≥ C).
выполняется неравенство x ≤ C (x ≥ C).
Множество, ограниченное и сверху, и снизу называется ограниченным.
Наименьшее из чисел, ограничивающих множество X сверху, называется точной верхней гранью данного множества. (sup X)
Наибольшее из чисел, ограничивающих множество X снизу, называется точной нижней гранью данного множества. (inf X)
Абсолютная величина числа–величина, определяемая след. обр.: 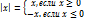
Свойства:  2. 2.  3. 3.  | |
4.  Док-во: Док-во:  + +   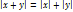 | 5.  Док-во: Док-во: 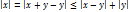  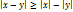 6. 6.  , ,   , ,  |
Функцией или отображением называется отображение из множества X в множество Y при α каждому элементу из множества X сопоставлен один и только один элемент множества Y.(y=f(x);  )
)
Способы задания: Аналитический,Графический, Словесный (вербальный),Табличный
1. Простейшие: а) y=const - постоянная б) y=kx+b – линейная в) y=  - степенная г) y= - степенная г) y=  - показательная (а≠1, а>0) д) y= - показательная (а≠1, а>0) д) y=  - логарифмическая е) y= - логарифмическая е) y= 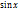 ; y= ; y=  ; y= ; y=  ;,y=ctg x - тригонометрическая ж) y= ;,y=ctg x - тригонометрическая ж) y= 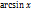 ; y= ; y=  y= y=  ; y=arcctg x – обратная тригонометрическая 2. Элементарная функция – функция полученная с помощью четырех арифметических действий, а так же операций взятия функции от функции. ( ; y=arcctg x – обратная тригонометрическая 2. Элементарная функция – функция полученная с помощью четырех арифметических действий, а так же операций взятия функции от функции. ( ) ) | 3. Целые алгебраические функции:  4. Дробно-рациональные функции: 4. Дробно-рациональные функции:  5. Иррациональные функции. ( 5. Иррациональные функции. (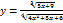 ) 6. Функция не являющееся дробно-раиоальной или рациональной называются трансцендентной. ) 6. Функция не являющееся дробно-раиоальной или рациональной называются трансцендентной. |
 2017-10-25
2017-10-25 998
998








