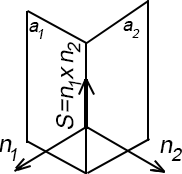
 Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей.
Прямую в пространстве можно задать как линию пересечения двух непараллельных плоскостей.
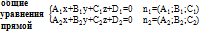
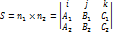 Каноническое уравнение прямой:
Каноническое уравнение прямой: 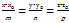
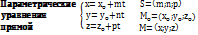
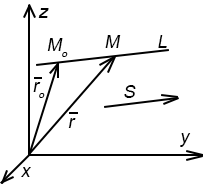
Векторное уравнение прямой: r=ro+tS L||S
t- скалярный множитель (параметр)
tS=MoM
 20. Взаимное расположение прямых и плоскостей в пространстве
20. Взаимное расположение прямых и плоскостей в пространстве
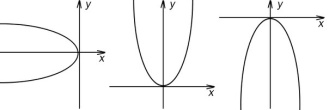
Условие параллельности прямых: q̅1 (l1, m1, p1), q̅2 (l2, m2, p2) 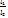 = = 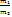 = =  Условие перпендикулярности прямых: q̅1; q̅2 l1 * l2 + m1 * m2 + p1 * p2 = 0 Условие параллельности плоскостей: n̅1 (A1; B1; C1); n̅2 (A2; B2; C2) Условие перпендикулярности прямых: q̅1; q̅2 l1 * l2 + m1 * m2 + p1 * p2 = 0 Условие параллельности плоскостей: n̅1 (A1; B1; C1); n̅2 (A2; B2; C2) 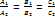
| Условие перпендикулярности плоскостей: n̅1; n̅2
A1A2 + B1B2 + C1C2 = 0 Условие параллельности прямой и плоскости: q̅ (l, m, p); n̅ (A; B; C) Al + Bm + Cp = 0 Условие перпендикулярности прямой и плоскости: q̅; n̅

|
| Синус угла между прямой и плоскостью: | |
L: 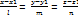 ; Q: Ax + By + Cz + D = 0 sinɸ = ; Q: Ax + By + Cz + D = 0 sinɸ = 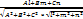
| 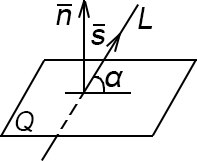 n̅ = (A; B; C) S̅ = (l; m; n) ɸ - угол между
плоскостями Q и L n̅ = (A; B; C) S̅ = (l; m; n) ɸ - угол между
плоскостями Q и L
|
 21. Линии второго порядка
21. Линии второго порядка
Общее ур-ние линий второго порядка имеет вид:
Ax2 + 2Bxy + Cy2 + 2Dx + 2Dy + F = 0, где A, B, C, D, E, F - коэфф., прин. R
В зависимости от коф-та линии второго порядка разделяются на окружности, элипсы, гиперболы и параболы.
Окружность при А=С.
- это множество всех равноудалённых точек
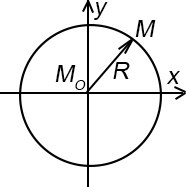
M0 (x0; y0)
M (x; y) (x - x0)2 + (y - y0)2 = R2
x2 + y2 - 2x0x - 2y0y + x02 + y02 - R2 = 0
B = 0; A = C
Эллипс при A * C > 0
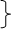 - наз. множество всех точек плоскости, сумма расстояний которых до 2 данных точек называется фокусом, есть величина постоянная.
- наз. множество всех точек плоскости, сумма расстояний которых до 2 данных точек называется фокусом, есть величина постоянная.
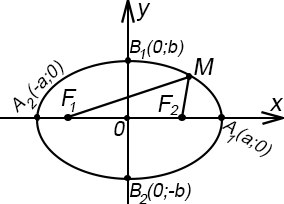
F1 (-C; 0) |F1M| + |F2M| = 2a
F2 (C; 0) |F1M| = 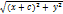 фокальные
фокальные
M (x; y) |F2M| =  радиусы
радиусы
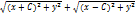 = 2a
= 2a
(после действий над ур-ниями получаем)
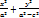 = 1 b2 = a2 - c2 →
= 1 b2 = a2 - c2 → 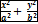 = 1
= 1
| О - центр элипса, А1А2 - большая ось, В1В2 - малая ось, | ОА1 = ОА2 – большая полуось, ОВ1 = ОВ2 - малая полуось |
Форма элипса зависит от отношения  (b = a элипс превр. в окр.)
(b = a элипс превр. в окр.)
E =  - эксцентриситет элипса (E - эпсилон) 0 < E < 1
- эксцентриситет элипса (E - эпсилон) 0 < E < 1
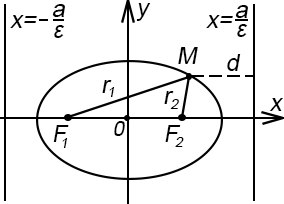
r1 = A + Ex и r2 = a – Ex; x = ±  - директрисы элипса; r - либо
- директрисы элипса; r - либо 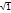 , либо
, либо 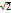
 = E
= E



 Гипербола при А * С < 0
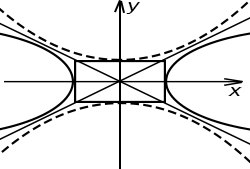
Гипербола при А * С < 0
наз. множество всех точек плоскости, модуль разности расстояний которых до двух равных точек наз. фокусами, есть величина постоянная.
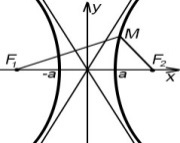 M (x; y) | |F1M| - |F2M| | = 2a
M (x; y) | |F1M| - |F2M| | = 2a
F1 (-C; 0) |F1M| = 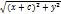
F2 (C; 0) |F2M| = 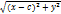
После возвед. выражения в квадрат и сделав пробразования, получим: 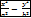 = 1 каноническое ур-ние, при b2 = c2 - a2
= 1 каноническое ур-ние, при b2 = c2 - a2
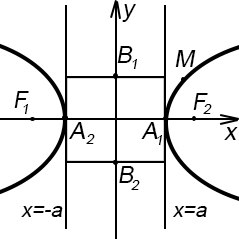
O (0; 0) - центр гиперболы
A1 (a; 0) и A2 (-a; 0) - вершины гип.
|A1A2| = 2a - действит. ось
|OA1| = |OA2| = a - действит. полуось
B1 (0; b) и B2 (0; - b) - мнимая ось
|OB1| = |OB2| - мнимая полуось
прямоуг. со сторонами 2a и 2b
над основным прямоуг. гиперболы
y = ±  x - это асимптоты
x - это асимптоты
E =  - эксцентриситет гиперболы (E > 1)
- эксцентриситет гиперболы (E > 1)
x = ±  - директрисы гиперболы
- директрисы гиперболы
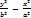 = 1 и
= 1 и 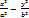 - сопряжённые
- сопряжённые
Парабола при A * C = 0
наз. множество всех точек плоскости, которые равно отдалены от точки назыв. фокусом и прямой назыв. директрисой, которое не проходит через фокус.
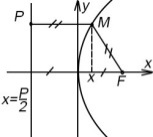 M (x; y) по определ. |MP| = |FM| E = 1
M (x; y) по определ. |MP| = |FM| E = 1
F ( ; 0)
; 0) 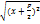 =
= 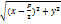
P (- 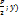 y2 = 2 px
y2 = 2 px
каноническое ур-ние
y2=-2px x2=2py x2=-2py
 2017-10-25
2017-10-25 677
677








