2017-10-25
4809
Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число 
, то говорят, что задана числовая последовательность 
Для любого 
существует номер, зависящий от эпсилонта, такой, что для всех членов последовательности с номерами больше, чем этот номер выполняется неравенство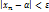 
, 
.
Последовательность, имеющая предел называется сходящейся, при этом все арифметические действия производятся только со сходящимися последовательностями.
Теорема1: сходящиеся последовательности имеют единственный предел)
Док-во: Пусть 
имеет предел b≠a,
|
| x |
| a |
| b |
|
|
|
окрестности не имеют общих точек, тогда по определению предела в эпсилон окрестности точки А содержится бесконечно много членов последовательности 
, а вне этой окрестности конечное число членов, тогда точка В не может быть пределом последовательности.
Теорема 2: сходящаяся последовательность ограничена.
Док-во: Из определения последовательности, можно записать 
,
. Так как модуль суммы не превосходит суммы модулей, то
, тогда 
Положим 
, 
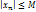, т.е. последов-ность ограничена.
3.Бесконечно-большие и бесконечно-малые последовательности. Теоремы о сумме (разности), произведении и частном двух сходящихся последовательностях. Предельный переход в неравенствах. Монотонные последовательности. Число ℮. Предел функции. Теоремы о пределах функции.
Последовательность  наз. бесконечно большой, если 
справедливо  . 
| Последовательность называется бесконечно малой, если 
справедливо  .
|
Теорема 1: Если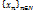 
бесконечно большая, то 
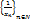является бесконечно малой и наоборот, если бесконечно малая, то 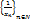бесконечно большая.
Док-во: Пусть бесконечно большая,
т.е. и . 
, тогда , 
,, 
.
- бесконечно большая; 
- бесконечно малая.
Теорема 2: Если последовательность 
и 
бесконечно малые, то
, бесконечно малая (
).
Док-во: 
; 
, 
;
- бесконечно малая.
Теорема 3: Произведение двух бесконечно малых последовательностей есть последовательность бесконечно малая. (
) Док-во:
; 
, 
,
– бесконечно малая последовательность.
Теорема 4: Произведение ограниченной последовательности на бесконечно малую есть последовательность бесконечно малая. (
Док-во: – ограниченная; , 
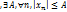
– бесконечно малая; 
; 
, 
– бесконечно малая послед-ость.
Следствие: Если имеет предел равный А, то это означает, что 
-бесконечно малая последовательность.
Справедливо и обратное: Если -бесконечно малая последовательность, то имеет предел равный А.
Теорема о сумме (разности): Сумма (разность) двух сходящихся последовательностей есть последовательность сходящаяся, предел которой равен сумме (разносте) пределов этих последовательностей. (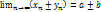
)
Док-во: 
- бесконечно малая; 
- бесконечно малая
; 
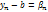, тогда 
и 
.
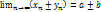Теорема о произведении: Произведение двух сходящихся последовательностей есть последовательность сходящаяся, предел которой равен произведению пределов этих последовательностей. 
0 Док-во: и
| Бесконечно малая |
– бесконечно малая, тогда 
.
Теорема о частном: частное двух сходящихся последовательностей есть последовательность сходящаяся, предел которой равен частному пределов этих последовательностей.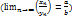 
Док-во: аналогично двум предыдущим!
Предельный переход к неравенствам:
Теорема 1: Если все члены последовательности удолетворяют неравенству 
, то предел последовательности a ≥b.
Теорема 2 (теорема о двух полицейских – о сжатой переменной): Если последовательности 
, и 
, и 
удовлетворяют 
.
Монотонные последовательности:
1.  послед-ость возврстающая
2.  послед-ость неубывающая
| 3.  послед-ость убывающая
4. 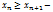 послед-ость невозврста-ая
|
!Монотонная ограниченная последовательность сходится.
Число e: 
(неперовое число)
, 
; 
; …; 
;…. 
.
Предел f(x) определена в некоторой окрестности точки, за исключением только если самой точки.
1. По Гейне: Число А называется пределом функции f(x) при 
, если для любой последовательности сходящийся к 
, последовательность значений функции 
сходится к А. (
2. По Каши: Число А называется пределом функции 
.
Односторонним предел: Число А называется пределом функции f(x) справа при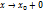 
, если 
, такое что 
, то 
.(
: Число А называется пределом функции f(x) слева при 
, если , такое что 
, то . (
)
Предел функции при 
:
Число А называется пределом функции (x) при , если 
.
Теоремы о пределах функции:
Теорема 1: Если f(x), g(x) при имеют предел А и В, то 
соответственно имеют пределы А±В, 
.
Теорема 2 (о сжатой переменной): Если функции f(x) и 
, и 
удовлетворяют 
.
