2017-10-25
759
- второй замечательный предел
Док-во: 1.Пусть 
. Каждое значение α заключено между двумя положительными целыми числами: n ≤ α ≤ n+1, где n=[α] – целая часть α, тогда 
.
, 
По теореме о сжатой переменной 
2.Пусть 
, при этом 
, тогда
6.Бесконечно-большие и бесконечно‑ малые функции. Сравнение бесконечно‑малых функций. Асимптотические формулы.
1.Функция у=f(x) называется бесконечно большой при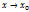 
, если
(
)
2. Функция у=f(x) называется бесконечно большой при 
, если
(
)
; 
Функция у=f(x) называется бесконечно малой при 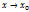, если 
.
Теорема о сумме бесконечно малых функций: Если α(x) и β(x) называют бесконечно малыми, то функция α(x)+β(x) так же бесконечно малая.
Теорема об эквивалентности: Если α(x), 
и β(x) называют бесконечно малыми при 
, при чем 
, то 
.
Теорема необходимого и достаточного условия эквивалентности: Для того что бы α(x) и β(x) были эквиваленты при , необходимо и достаточно, что бы их разность была бесконечно малой более высшего порядка, чем каждая из этих функций.
Сравнение бесконечно малых функций:
1.Если  , то α(x) наз. бесконечно малой более высоко порядка при сравнение с β(x) при . | 3. Если  , то α(x) и β(x) наз. бесконечно малыми одного порядка. |
2.Если  , α(x) и β(x) наз. эквивалентными. | 4.. Если  , то α(x) наз. бесконечно малой более низкого порядка при сравнение с β(x) при x→xo |
Асимптотические формулы:
1. 
2. 
3. 
4. 
5. 
6. 
