Среднее арифметическое

Преподаватель: Платонова Татьяна Евгеньевна

Математическая статистика

Лекция 1

Основные понятия математической статистики

Математическая (или теоретическая) статистика опирается на методы и понятия теории вероятностей, но решает в каком-то смысле обратные задачи.

В теории вероятностей рассматриваются случайные величины с заданным распределением или случайные эксперименты, свойства которых целиком известны. Предмет теории вероятностей — свойства и взаимосвязи этих величин (распределений).

Но часто эксперимент представляет собой черный ящик, выдающий лишь некие результаты, по которым требуется сделать вывод о свойствах самого эксперимента. Наблюдатель имеет набор числовых (или их можно сделать числовыми) результатов, полученных повторением одного и того же случайного эксперимента в одинаковых условиях.

При этом возникают, например, следующие вопросы: Если мы наблюдаем одну случайную величину — как по набору ее значений в нескольких опытах сделать как можно более точный вывод о ее распределении?

Если мы наблюдаем одновременно проявление двух (или более) признаков, т.е. имеем набор значений нескольких случайных величин — что можно сказать об их зависимости? Есть она или нет? А если есть, то какова эта зависимость?

Часто бывает возможно высказать некие предположения о распределении, спрятанном в «черном ящике», или о его свойствах. В этом случае по опытным данным требуется подтвердить или опровергнуть эти предположения («гипотезы»). При этом надо помнить, что ответ «да» или «нет» может быть дан лишь с определенной степенью достоверности, и чем дольше мы можем продолжать эксперимент, тем точнее могут быть выводы. Наиболее благоприятной для исследования оказывается ситуация, когда можно уверенно утверждать о некоторых свойствах наблюдаемого эксперимента — например, о наличии функциональной зависимости между наблюдаемыми величинами, о нормальности распределения, о его симметричности, о наличии у распределения плотности или о его дискретном характере, и т.д.

Итак, о (математической) статистике имеет смысл вспоминать, если

· имеется случайный эксперимент, свойства которого частично или полностью неизвестны,

· мы умеем воспроизводить этот эксперимент в одних и тех же условиях некоторое (а лучше — какое угодно) число раз.

Примером такой серии экспериментов может служить социологический опрос, набор экономических показателей или, наконец, последовательность гербов и решек при тысячекратном подбрасывании монеты.

Лекция 2.

Первичная обработка результатов эксперимента

Среднее арифметическое

Дисперсия и среднее квадратическое отклонение

Интервальный ряд и гистограмма

Первичная обработка результатов эксперимента

Явления, происходящие в природе и обществе, сложны и разнообразны. Ученые изучают разные стороны этих явлений, причем каждая наука вырабатывает свои методы исследования. Например, преступность изучают юристы, социологи, психологи, медики. Есть тут серьезная работа и для математиков. Их задача – подвергнуть математической обработке огромный статистический материал – отчеты органов внутренних дел и прочее – содержащий различные числовые данные. Цель этой работы – выделить наиболее существенные сведения об интересующем явлении.

Результаты обработки представляются в виде таблиц, диаграмм, графиков и различных числовых характеристик, которые называются параметрами. Важнейшие из них – среднее арифметическое и дисперсия.

Среднее арифметическое

Понятие среднего значения используется для описания разнообразных явлений природы и общественной жизни: средняя температура воздуха, средняя зарплата, средняя продолжительность жизни. Например, для изучения общественного мнения проводят опрос не всех избирателей, а лишь небольшой части населения. По результатам прогнозируют популярность кандидатов у различных групп населения в разных регионах. При грамотной математической обработке результатов опроса выводы будут достаточно точно отражать реальную ситуацию.

Средней величиной обычно называют среднее арифметическое.

Пусть - некоторые числа. Их средним арифметическим называется число

(1)

Пример. Количество ДТП на улицах города в первую декаду декабря:

6 8 10 7 6 11 9 8 7 11.

Среднее арифметическое этих чисел

показывает среднее число ДТП в день.

В сводке за следующие 10 дней такие данные: 0 5 7 7 12 11 14 13 7 6.

Их среднее арифметическое

Отсюда видно, что средние значения 8,3 и 8,2 отличаются друг от друга значительно меньше, чем число ДТП за каждый день. Поэтому среднее число ДТП можно прогнозировать, причем достаточно точно. Этот факт подтверждается и отчетами ГАИ за много лет. Из них также видно, что чем больше срок отчетности (декада, месяц, квартал, …), тем устойчивее средняя величина.

Такое свойство средних значений представляет собой одно из важнейших проявлений закона больших чисел, открытого знаменитым русским математиком П.Л.Чебышевым.

Если исходные данные содержат несколько десятков чисел, то составляют таблицу, в которой указывают для каждой величины, сколько раз она наблюдалась.

Пример. Число правонарушений в городе, совершенных подростками за первые 20 дней сентября: 8 6 13 4 13 13 12 9 7 6 12 14 13 12 17 6 8 12 7 12. По этим данным составим таблицу:

Таблица 1

Здесь - число дней с одинаковым количеством правонарушений, - число правонарушений за день. В первой строке значения расположены в порядке возрастания, а если сложить все числа второй строки, то получится общее число дней, т.е. 20.

Среднее число правонарушений в день:

Отсюда формулу (1) можно переписать так:

(2)

Здесь - различные среди заданных n чисел.

При этом 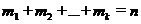(3)

Таблицу 1 можно переписать так, чтобы во второй строке вместо числа дней стояла доля, которую это число составляет от числа всех дней, т.е. частота:

Таблица 2.


	0,05	0,15	0,1	0,1	0,05	0,25	0,2	0,05	0,05

Используя понятие частоты, подсчитаем среднее значение иным способом:

Таким образом, среднее арифметическое равно сумме произведений чисел, взятых из первой строки таблицы 2, на их частоты.

Преобразуем таким же способом формулу (2). Возьмем частоты:

; ;…;

Отсюда (4)

Этой формулой можно пользоваться и в том случае, когда не известны величины , но известны значения частот.

Пример. В некотором городе каждому пассажиру междугородного автобуса вручают страховой полис на 50000 руб., взимая за это 50 руб. Какова средняя прибыль страховой компании от продажи одного полиса, если несчастные случаи происходят в среднем с одним пассажиром из 10000?

Решение. Прибыль может принимать 2 значения: 50 руб., если несчастного случая не произошло, и – 49950 руб. при гибели пассажира. Составим таблицу частот: