Меры средней тенденции и отвечающие им модели

Итак, мы получили частотное распределение значений рассматриваемого признака, т.е. выборочное представление изучаемой одномерной случайной величины. Конечно, анализ этого распределения может много дать социологу. Именно с расчета таких распределений для всех рассматриваемых признаков (так называемых “линеек”) он обычно и начинает анализ данных. Каждое распределение представляет собой своеобразное описание изучаемой совокупности объектов (респондентов). Такие описания позволяют исследователю лучше сориентироваться в проблематике, скорректировать перечень проверяемых гипотез, уточнить априорные представления об объекте и предмете исследования. Но этим анализ каждого одномерного распределения обычно не ограничивается.

Оказывается, что даже для одномерных случайных величин можно найти целый ряд статистических закономерностей. Конечно здесь они довольно примитивны (скажем, мы не можем говорить о связях между переменными), но все же это - статистические закономерности. В первую очередь мы имеем в виду так называемые меры средней тенденции, среди которых (в математической статистике известно бесконечное количество таких мер, им посвящена довольно обширная литература, см., например, [Джини, 1970]). в социологии наиболее часто используются математическое ожидание, мода и квантили (наиболее употребительным квантилем является медиана). Их мы и рассмотрим, полагая, что необходимость использования этих мер социологом очевидна. Подчеркнем лишь, что каждая из этих мер – некоторое значение (единственное!) рассматриваемого признака, которое должно характеризовать, как бы подменять, всю нашу совокупность. И социолог должен проявлять повышенное внимание к тому, чтобы с содержательной точки зрения такая подмена была оправданной.

Напомним, что названные средние являются параметрами распределения вероятностей. Не будем давать их строгого определения для генеральной совокупности. Опишем лишь то, как они измеряются для выборки. Говоря более грамотно, мы покажем, каковы выборочные точечные оценки указанных параметров, или, что то же самое, опишем способы расчета отвечающих этим параметрам выборочных статистик. (Напомним, что выборочные оценки параметров распределения делятся на точечные, когда для выборочных данных находится одно значение, служащее оценкой генерального параметра, и интервальные, когда на базе выборочной точечной оценки параметра строится так называемый доверительный интервал. Определенная на выборке переменная, значениями которой служат точечные оценки какого-либо параметра, называется статистикой, отвечающей этому параметру. Соответствующий материал обычно изучается в курсе математической статистики; см. также [Гласс, Стэнли, 1976; Статистические методы..., 1979].)

Все описываемые ниже меры средней тенденции являются "хорошими" выборочными точечными оценками генеральных параметров (напомним, что "хорошей" оценкой в математической статистике называются оценки, являющиеся несмещенными, состоятельными, эффективными; не будем напоминать, что это такое; отметим только, что выполнение указанных свойств

дает исследователю возможность с наибольшей вероятностью избежать сильного отклонения наблюденного значения статистики от соответствующего генерального параметра).

Пусть x₁, x₂,..., x_N – выборочные значения рассматриваемого признака (N – объем выборки). Статистикой, отвечающей математическому ожиданию (дающей “хорошие”. точечные выборочные оценки этого параметра; это также – материал курса математической статистики) является знакомое всем среднее арифметическое значение признака:

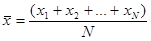
Среднее арифметическое значение признака, вычисленное для какой-либо группы респондентов, чаще всего интерпретируется как значение для наиболее типичного для этой группы человека, это среднее значение как бы служит "олицетворением" этой группы (по качеству, связанному с рассматриваемым признаком). Однако бывают случаи, когда подобная интерпретация среднего арифметического несостоятельна. Ниже мы рассмотрим некоторые из них.

Напомним, что квантиль – это такое значение признака q, которое делит диапазон его изменения на две части так, чтобы отношение числа элементов выборки, имеющих значение признака, меньшее q, к числу элементов, имеющих значение признака, большее q, было равно заранее заданной величине. Среди всех возможных квантилей обычно выделяют определенные семейства. Квантили одного семейства делят диапазон изменения признака на заданное число равнонаполненных частей. Семейство определяется тем, сколько частей получается. Наиболее популярными квантилями являются квартили, разбивающие диапазон изменения признака на 4 равнонаполненные части; децили - на 10 равнонаполненных частей; процентили – на 100 частей. Символически эти определения можно изобразить следующим образом.

Квартили:

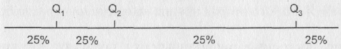
Децили:

Процентили:

Рис. 10. Иллюстрация сущности наиболее употребительных квантилей.

Величина процента, указанная под интервалом означает долю объектов выборки, попавших в этот интервал.

Разного рода квантилями социолог пользуется очень часто. Нередко они упоминаются в средствах массовой информации (однако при этом сами термины "квантиль", "квартиль" и т.д. при этом не используются). Так, в газетах пишут о том, что, например, 10% наиболее богатых "россиян" имеют месячный доход свыше 100 тысяч рублей, а 10% наиболее бедных – ниже 300 рублей. Ясно, что 100 тысяч рублей – это девятый дециль D₉, а 300 рублей – это первый дециль D₁.

Медианой называется Мe = Q₂ = D₅ = Р₅₀.

Нетрудно видеть, что так определенная выборочная медиана – это значение рассматриваемого признака, которое делит отвечающий этому признаку вариационный ряд (т.е. последовательность значений признака, расположенных в порядке их возрастания) пополам. Иначе говоря, медиана обладает тем свойством, что половина всех выборочных значений признака меньше нее, а половина – больше. "Правомочность" медианы в качестве представителя анализируемой группы респондентов представляется очевидной. Для того, чтобы это почувствовать, достаточно "взглянуть", скажем, на две группы, в одной из которых медиана признака "доход" равна 500 рублей, а в другой – 5000 рублей. Ясно, что вторая группа "в среднем" гораздо богаче первой.

Обычно, построив вариационный ряд, полагают, что при нечетном числе элементов в выборке медиана равна центральному члену ряда, а при четном – точке, отвечающей середине расстояния между двумя центральными членами.

Нетрудно видеть, что вычисление медианы имеет смысл только для порядкового признака (и, конечно, для интервального, поскольку любая интервальная шкала является порядковой). Это представляется очевидным: для “чисто” номинальной шкалы (т.е. для такой, при использовании которой мы не ставим своей целью отображение какого бы то ни было эмпирического отношения порядка в числовое) само выражение “объект обладает значением признака, меньшим, чем медиана” становится бессмысленным. Понятия “больше” или “меньше” в этой ситуации не существуют

В случае же, когда медиана вычисляется как середина между двумя шкальными значениями, мы делаем фактически еще одно предположение – о том, что наш порядковый признак в принципе может принимать значения, лежащие между используемыми пунктами шкалы.

Можно рассчитывать медиану и с помощью построения кумуляты. Это также опирается на предположение о непрерывности рассматриваемого признака. Более того, здесь работает еще одно модельное предположение: объекты внутри каждого интервала распределены равномерно. Подчеркнем, что этот пример хорошо иллюстрирует то, что за каждым математическим методом, даже самым простым, стоит своя модель изучаемого явления. В данном случае - модель понимания средней тенденции. Разбив диапазон изменения признака на интервалы и простроив полигон плотности распределения, мы потеряли информацию о том, как в действительности расположены объекты внутри каждого интервала, и заменили эту информацию модельным предположением, состоящим в том, что соответствующее распределение равномерно.

То, как находятся квантили с помощью кумуляты, подробно описывается, например, в [Паниотто, Максименко, 1982; Толстова, 1998; Ядов, 1998]. Мы не будем на этом подробно останавливаться. Надеемся, что суть подхода станет ясной из рис. 11.

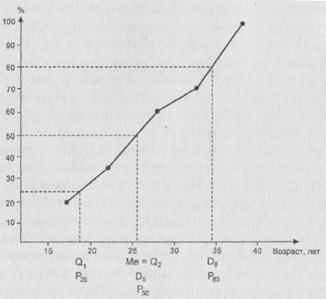
Рис. 11. Иллюстрация одного из возможных способов расчета квантилей

Эквивалентным этому подходу является расчет квантилей по формулам, приведенным в [Рабочая книга..., 1983. С. 161]. Более подробно о разных способах расчета медианы и о сути используемых при этом моделей см. Приложение 1 (на наш взгляд, рассмотрение соображений, описанных в этом Приложении, может способствовать лучшему пониманию, что такое модель, заложенная в методе).

Модой называется наиболее часто встречающееся значение признака. Нахождение моды обычно не представляет трудностей. Ясно, что ее можно рассчитывать для признаков, измеренных по шкалам любых рассматриваемых нами типов. (Иногда моду предлагается рассчитывать по определенной формуле [Рабочая книга..., 1983. С.162]. Но это сопряжено с довольно сильными модельными предположениями; в частности, признак должен быть порядковым и непрерывным).

Надеемся, что читателю ясно, почему моду относят к мерам средней тенденции. Приведем пример. Сравнивая, скажем, распределение по профессиям, рассчитанные для двух регионов – Ивановской и Тюменской области, мы можем придти, например, к выводу, что в первой наиболее распространенная профессия – ткачиха, а во второй – нефтяник. Этот вывод означает, что ткачиха – модальное значение профессии для жителей Ивановской области, а нефтяник – для Тюменской. И соответствующее первичное описание этих областей, т.е. как бы условное отождествление первой области с ткачеством, а второй – с добычей нефти, является вполне естественным.

Подчеркнем, что, при всей своей простоте, описанные статистики – это все же статистические закономерности, и при их расчете и интерпретации возникает множество тех же методических проблем, что и при использовании сложных многомерных методов анализа. Мы не можем уделить таким проблемам достаточное внимание при рассмотрении всех затрагиваемых ниже методов. Коротко коснемся их лишь применительно к тем простейшим статистическим закономерностям, о которых идет речь в настоящем параграфе. А именно, обратим внимание читателя на следующие, не всегда замечаемые методические аспекты использования мер средней тенденции, пытаясь по возможности обобщить соответствующие положения на ситуации, возникающие при изучении статистических закономерностей произвольного вида.

Как мы уже отметили, любая средняя – это параметр распределения соответствующей случайной величины (либо статистика, вычисленная для выборочного частотного распределения рассматриваемого признака). И здесь мы сталкиваемся с общим положением - все известные методы нахождения статистических закономерностей являются методами расчета некоторых параметров рассматриваемых распределений (не обязательно одномерных), любая закономерность может быть выражена через ту или иную совокупность параметров. И для всех таких параметров встает задача их точечного и интервального оценивания. Для средних величин способы решения этой задачи известны [Гласс, Стэнли, 1976; Гмурман, 1998а; Калинина, Панкин, 1998; Статистические методы..., 1979]. Однако для многих интересующих социолога параметров не разработана та теоретическая основа, которая дает возможность построения интервала. В таких случаях социолог, вообще говоря, лишается возможности переносить результаты с выборки на генеральную совокупность. Правда, как мы уже отмечали в п.4.1 части I, современная наука предоставляет некоторый способ преодоления этой трудности – использование специальным образом организованной процедуры моделирования большого числа выборок на ЭВМ, наблюдение получающихся при этом распределений рассматриваемых статистик (для каждой выборки - свое значение статистики), вычисление параметров этих распределений и построение на этой основе требующихся доверительных интервалов.

Далее, любая статистическая закономерность – это своего рода сжатие исходных данных. Это ярко видно на примере средних величин. Так, при использовании среднего арифметического мы вместо набора, скажем, из 1000 значений возрастов мы получили одно число – 32,4, средний возраст респондентов рассматриваемой совокупности. Совокупность из тысячи чисел сжата в одно число.

Указанное сжатие означает потерю информации. С такой потерей связано нахождение любой закономерности (коротко об этом уже шла речь в п.1.4 части I). Анализируя данные, мы всегда сталкиваемся с парадоксом: только потеряв определенную информацию, мы можем приобрести новое знание (содержащееся в найденной закономерности). И интерпретируя найденное статистическое соотношение, постоянно надо давать себе отчет в том, что мы теряем. Так, пользуясь упомянутым выше средним значением, мы как бы забываем про то, что в нашей совокупности могут находиться люди весьма различного возраста. Она для нас начинает ассоциироваться с возрастом 32,4 года, мы как бы полагаем, что именно такой возраст имеет наиболее типичный представитель совокупности. А это может не отвечать действительности.

Следующее обстоятельство касается того, что любая статистическая закономерность имеет смысл лишь при определенной однородности той совокупности объектов, для которой эта закономерность рассчитывается. Понятие однородности сложно и многогранно [Толстова,1991а]. В нем имеются аспекты, как не зависящие от того, какую закономерность мы ищем, так и “привязанные” к конкретному методу анализа данных. И отнюдь не для всех важных для социолога методов эти аспекты изучены. Но средним в этом смысле “повезло”. В названной выше работе приведен перечень публикаций, в которых анализируется проблема однородности для среднего арифметического. Интуитивно ясно, о чем здесь идет речь: нельзя считать среднюю температуру по больнице и на этой основе сравнивать работу разных медицинских учреждений. Нельзя считать среднюю зарплату по какому-либо региону, если различие между высокооплачиваемыми и низкооплачиваемыми людьми слишком велика. В таком случае средняя зарплата не будет информативна. И на ее основе нельзя будет сравнивать, скажем, обеспеченность населения двух регионов.

Как мы отмечали в п.4.3 части I, одним из основных свойств социологических данных, обусловливающих специфические моменты в использовании социологами математической статистики, является то, что эти данные зачастую бывают получены по шкалам низких типов, из которых мы рассматриваем номинальные и порядковые. Метод анализа данных необходимо сопрягать с типом используемых шкал. Результаты применения метода должны быть инвариантными относительно применения к исходным данным допустимых преобразований тех шкал, по которым эти данные получены. Это свойство метода в работе [Толстова, 1998] называется его формальной адекватностью.

В свете этого можно сказать, что моду можно вычислять для шкал любых типов, начиная с номинального – объект, обладающий модальным значением, не будет изменяться при любом взаимно-однозначном преобразовании исходных шкальных значений (как известно, эти преобразования являются допустимыми для номинальных шкал). Значит, любые выводы, полученные на основе анализа мод, будут удовлетворять сформулированному выше свойству инвариантности.

Для того, чтобы имел смысл расчет медианы и других квантилей, шкала, как мы уже упоминали, должна быть по крайней мере порядковой. Легко показать, что все выводы на базе анализа квантилей останутся без изменения, если к исходным данным применить монотонно возрастающее преобразование (допустимое преобразование порядковых шкал).

Нетрудно понять, что среднее арифметическое неявно предполагает использование шкалы, отвечающей по крайней мере интервальному уровню измерения. Действительно, среднее арифметическое – это такое значение признака, для которого сумма расстояний от него до объектов, имеющих большее значение, равна сумме расстояний до объектов, имеющих меньшее значение. Это легко вытекает из соотношения:

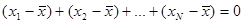
В этом – суть рассматриваемой статистики. Стало быть, эта самая суть требует осмысленности соотношений между расстояниями от одних значений признака до других.

Перейдем к рассмотрению свойств среднего арифметического, связанных с допустимыми преобразованиями шкал. Большинство соотношений (но не все!) между средними арифметическими, используемых в реальных социологических исследованиях, остаются инвариантными относительно положительных линейных преобразований исходных данных – допустимых преобразований интервальных шкал. Таковы, например, соотношения вида:

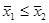
где x₁ и x_2, средние арифметические значения рассматриваемого признака, вычисленные для каких-либо двух подсовокупностей объектов (подробнее об этом см., например, [Клигер и др., 1978; Орлов, 1985]). Другими словами, большинство соотношений, включающих в себя среднее арифметическое, являются формально адекватными для интервальных шкал. Нетрудно показать, что для порядковых шкал, напротив, большинство подобных соотношений не будут формально адекватными (см. там же). Казалось бы, очевидным является и такое же утверждение для номинальных шкал. Но здесь требуется оговорить один момент.

Конечно, использование среднего арифметического, скажем, для чисел – кодов профессий респондента является бессмысленным. Тем не менее, бывают случаи, когда и для номинальных данных оказывается возможным использование этой статистики. Мы имеем в виду дихотомические номинальные признаки, принимающие два значения – 0 и 1. В соответствующей ситуации становится реальной вполне разумная интерпретация рассматриваемой статистики. Поясним это на примере.

Рассмотрим самый популярный дихотомический признак – пол респондента: 0 - мужчина, 1 - женщина.

Предположим, что у нас 10 респондентов со следующими значениями пола:

0, 0, 1, 1, 1, 0, 0, 0, 0, 1.

Нетрудно видеть, что соответствующее среднее арифметическое равно 0,4. Если мы будем его интерпретировать так, как обычно интерпретируют эту статистику, т.е. как пол некоего “среднего человека”, наиболее типичного представителя совокупности, то мы вряд ли получим что-либо осмысленное: наиболее типичным представителем совокупности, состоящей из здоровых мужчин и женщин, является человек, на 40% являющийся женщиной, на 60% мужчиной? Но оказывается, что возможна еще одна довольно естественная интерпретация нашего значения среднего арифметического: оно означает, что в изучаемой совокупности имеется 40% людей с единичным значением рассматриваемого признака (в данном случае - 40% женщин). Такой интерпретацией вполне можно пользоваться, не рискуя придти к нелепости.

Описанная ситуация весьма существенна для социолога. Как мы покажем ниже (см. п. 2.5 раздела 2), не только средние арифметические, но и многие другие статистики, вычисленные для дихотомических данных, поддаются столь же естественной интерпретации в виде некоторых процентов. А это дает основания использовать “числовой” анализ данных для изучения номинальной информации.

Как известно, формальной адекватности метода недостаточно для того, чтобы его можно было считать подходящим для решения той или иной конкретной задачи. Помимо формальной, требуется еще и содержательная адекватность. Метод, подходящий для используемых шкал, может не быть пригодным из содержательных соображений. Это касается и столь простых методов, как методы расчета мер средней тенденции. Пример был приведен в п.5.1 части I.

Содержательное сравнение описанных мер средней тенденции осуществляется во многих работах (см., например [Рабочая книга..., 1983; Гласс и Стэнли, 1976 ].

Наконец, последнее методическое положение, которое мы упомянем – это необходимость анализа модели, заложенной в методе. Применительно к мерам средней тенденции такие модели фактически уже были рассмотрены: эти модели включали в себя предположения о типе шкалы, отвечающей рассматриваемому признаку, о непрерывности признака, о расположении его значений внутри каждого интервала и т.д.