Задачи для самостоятельной работы. Проверить, истинны ли соотношения между множествами

 

Задача 1

Проверить, истинны ли соотношения между множествами:

1. А \ (В È С) = А \ В \ С.

2. (А \ В) È (В \ А) = (А È В) \ (А ∩ В).

3. А \ (В ∩ С) = (А \ В) È (А \ С).

4. А \ (А \ В) = (А ∩ В).

5. А \ (В \ А) = А \ В.

 

Этап формирования ПК-2. E. Определить порядок действий при вычислении значений суперпозиции элементарных функций

Решение типовой задачи

Условие задачи

Определение порядка действий при вычислении значения суперпозиции элементарных функций и простых многоместных функций

Z = .

 

Решение задачи

№ п/п	Алгоритм расчета	Конкретное действие в соответствии с алгоритмом
	Определить состав переменных и констант в формуле, которая задает функцию	Переменные X, Y; константа 1
	Определить внешнюю операцию (функцию) и основные подформулы	Z = , где . Z2 = XY2; Z3 = lg Z4. Z4 = Y2 +
	Определить, какие из функций, составляющих суперпозицию, являются одноместными, а какие – двуместными	Операции – одноместные; арифметические операции +, –, ×, / – двуместные
	Составить иерархическую схему последовательности действий	Z = . . Z2 = X · Z5 Z3 = lg Z4. Z4 = Z5 + Z6. Z5 = Y2. Z6 =

Задачи для самостоятельной работы

 

Задача 1

Определить порядок действий при вычислении значения суперпозиции элементарных функций и простых многоместных функций.

1. .

2. .

3. .

4. .

5. .

6. .

 

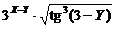Этап формирования ПК-2. F. Выяснить, является ли данное множество с определениями сложения/умножения группой, кольцом или полем. Определить, что является нейтральным элементом и обратным элементом