Примеры решения задач. Задача 1.Проверить справедливость равенства А (В Ç С) = (А В) Ç (А С)

Задача 1. Проверить справедливость равенства А \ (В Ç С) = (А \ В) Ç (А \ С).

Решение. Строим диаграммы Венна отдельно для множества, заданного в левой части проверяемого равенства, и для множества в правой части (рисунок 1).

Рисунок 1

В левой части пересечение (В Ç С) показано частой косой штриховкой, разность А \ (В Ç С) – редкой штриховкой. В правой части разность (А \ В) показана вертикальной штриховкой, разность (А \ С) – горизонтальной штриховкой, их пересечение (А \ В) Ç (А \ С) – область, заштрихованная дважды (в клеточку). Сравнение обоих рисунков показывает, что левая и правая части равенства – разные. Следовательно, равенство неверно: А \ (В Ç С) ≠ (А \ В) Ç (А \ С).

Из этих же чертежей можно заключить, что множество в левой части равенства совпадает с объединением двух разностей из правой части (А \ В) È (А \ С).

Задача 2. Опрос 100 студентов показал, что 52 пользуются домашним компьютером, 71 – мобильным телефоном, 12 – ни тем, ни другим. Сколько студентов используют оба прибора, только компьютер, только телефон?

Решение. Решение этой задачи связано с формулой числа элементов в объединении двух, вообще говоря, пересекающихся множеств: ½А È В½= ½А½ + ½В½ – ½А Ç В½.

Требуется выразить число элементов пересечения:

½А È В½= ½А½ + ½В½ – ½А Ç В½ Þ ½А Ç В½= ½А½ + ½В½ – ½А È В½.

Строим диаграмму Венна (рисунок 2). Из условия следует, что число элементов объединения равно 100 – 12 = 88. Результаты получаем подстановкой числовых данных в формулу:

½А È В½= 100 – 12 = 88;

½А Ç В½= 52 + 71 – 88 = 35;

½А \ В½= 52 – 35 = 17;

½В \ А½= 71 – 35 = 36.

Оба прибора используют 35 студентов, только компьютер – 17, только телефон – 36.

Задача 3. Что называется декартовым произведением двух множеств? Найти и показать на координатной плоскости произведение А В, где А = [3, 5], В = [1, 4]: А и В – множества либо дейcтвительных чисел R, либо натуральных чисел N: а) А, В Í N; б) A, B Í R; в) A Í N, B Í R;
г) A Í R, B Í N.

Рисунок 2

Решение. Декартово произведение А ´ В двух множеств – это множество всех пар (x, y), где
x Î A, y Î B.

На рисунке 3, а, б, в, г произведение А ´ В изображается прямоугольником, проекция кото-рого на ось абсцисс – множество А, а проекция на ось ординат – множество В.

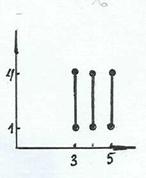
а) б) в) г)

Рисунок 3

Если же А и В – множества целых чисел А = [3, 5], В = (1, 4); А, В Í Z, то произведение
А ´ В – прямоугольник, составленный из целочисленных точек, т.е. точек, у которых обе координаты – целые числа (рисунок 8, а).

Для точек на рисунке 8, в, г одна из координат дискретная, другая – непрерывная.

Задача 4. Устанавливает ли функция y = cos x взаимно однозначное соответствие между отрезками [-π/2, π/2] и [0, 1]?

Решение. Используем графическое представление основной элементарной функции y = cos x (рисунок 4). На участке [–π/2, π/2] функция принимает все значения из отрезка [0, 1]. Но любое значение, кроме у = 1, функция принимает в двух точках: например, cos(–π/2) = cos(π/2) = 0.

Рисунок 4

Следовательно, взаимно однозначного соответствия на этом множестве нет.

Если же рассмотреть ту же функцию на множестве [0, π/3], то она осуществляет взаимно однозначное соответствие с отрезком [1/2, 1]. Это видно на графике.

Задача 5. Пусть f (X) = 2 ^X, g (X, Y) = X – Y. Что выражают суперпозиции h ₁(X, Y) = f (g (X, Y)), h ₂(X, Y) = g (f (Y), f (X)), h ₃(X) = f (g (X, f(X)))?

Решение. h ₁(X, Y) = f (g (X, Y)) = f (X – Y) = 2 ^X ^{- Y}.

h ₂(X, Y) = g (f (Y), f (X)) = f (Y) - f (X) = 2 ^Y - 2 ^X.

h ₃(X) = f (g (X, f (X))) = 2 ^g ^{(X, f (X))} = 2 ^X ^{- f (X)} = 2 ^X ^-.

Задача 6. x – вектор на плоскости; А(x), В(x) – одноместные алгебраические операции:
А(x) = х – b, где b = (2, 3); В(x) = 2 x. Какие векторы представляются суперпозициями этих операций A(A(x)), B(A(B(x))), A(B(A(x))), A(B(A(B(x)))), если х – вектор (5, 3)?

Решение. Применение операции A к вектору z - вычитание вектора (2, 3).

(А(x) = х – b = (5, 3) – (2, 3) = (3, 0).

Применение операции В к вектору z – удвоение. В(х) = 2∙ х = 2 × (5, 3) = (10, 6).

Далее – применение этих операций к результату предыдущей операции. На рисунке 5 – графическое представление суперпозиций.

А(А(x) = (х – b) – b = (3, 0) – (2, 3) = (1, –3).

А(В(x)) = (2 х – b) = (10, 6) – (2, 3) = (8, 3).

В(А(x)) = 2 × (х – b) = 2 × (3, 0) = (6, 0).

В(А(В(x))) = 2 × (2 х – b) = 2 × (8, 3) = (16, 6).

А(В(А(x))) = 2 × (х – b) – b = (6, 0) – (2, 3) = (4, -3).

А(В(А(В(x)))) = 2 × (2 х – b) – b = (16, 6) – (2, 3) = (14, 3).

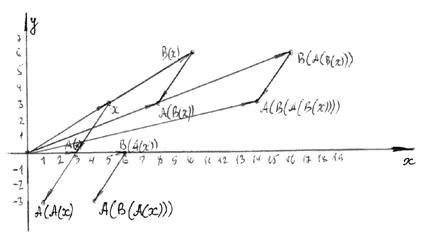
Рисунок 5

Задача 7. Пусть R – бинарное отношение на множестве М из 12 натуральных чисел
{4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24}: «x R y, если x ¹ y и х делится на у без остатка».

Сколько пар (x, y), элементы которых находятся в отношении x R y?

Является ли отношение x R y отношением эквивалентности?

Решение. Перечислим все такие пары: (8, 4), (10, 5), (12, 4), (12, 6), (15, 5), (16, 4), (16, 8),
(18, 6), (18, 9), (20, 4), (20, 5), (20, 10), (24, 4), (24, 6), (24, 8), (24, 12). Таким образом, их число – 16. Для ответа на вторую часть вопроса нужно проверить выполнение трех свойств, которыми должно обладать отношение эквивалентности. Транзитивность отношения выполняется: если x делится на y и y делится на z, то x делится на z; однако, рефлексивность отношения не выполняется в силу условия (отношение x R y не выполняется для равных x, y); отношение x R y также несимметрично: если x делится на y, то x > y, и поэтому y не делится на x. Следовательно, x R y не есть отношение эквивалентности.

Задача 8. Является ли отношение из предыдущей задачи отношением порядка?

Решение. Уточним результаты решения предыдущей задачи. Рассматриваемое отношение x R y транзитивно, антирефлексивно (не выполняется x R х) и антисимметрично (если x R y, то не выполняется y R x). Поэтому x R y – отношение строгого порядка.

Задача 9. Является ли упорядоченным или частично упорядоченным множество М с отношением x R y на нем из задач 8, 9?

Решение. Очевидно, не все пары элементов множества М сравнимы: например, 15 и 24, 10 и 18 и другие. Поэтому М – частично упорядоченное.

Задача 10. Пусть S(x, y, z) – трехместное отношение «x = y × z» на том же множестве М, что и в задаче 7: {4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24}. Сколько троек (x, y, z), элементы которых находятся в отношении S(x, y, z)?

Решение. Все тройки, удовлетворяющие заданным условиям: (16, 4, 4), (20, 4, 5), (20, 5, 4),
(24, 4, 6), (24, 6, 4); их число – 5. Заметим, что если y ¹ z, то (x, y, z) и (x, z, y) – разные тройки, но поскольку операция умножения коммутативна, то выполняется эквивалентность S(x, y, z) «S(x, z, y), т.е. вместе с каждой тройкой S(x, y, z) условию удовлетворяет и тройка S(x, z, y).