2017-12-16
1866
Применение дифференциала в приближенных вычислениях основано на замене приращения функции её дифференциалом 
. Абсолютная погрешность при такой замене равна 
и является при 
бесконечно малой более высокого порядка, чем 
.
Приращение функции 
может сложно зависеть от , и его вычисление часто сопряжено с большими трудностями. Вычисление же дифференциала по формуле 
просто. Геометрически замена приращения функции дифференциалом означает замену участка кривой в окрестности некоторой точки отрезком касательной к этой кривой в данной точке. Эта операция в математике получила название спрямление кривой или линеаризации.
Приближенное равенство применяется в основном в двух задачах:
1). Приближенном вычислении значения функции.
2). Оценке погрешностей в приближенных вычислениях.
Пусть известны значения функции 
в некоторой точке 
и её производной 
. Требуется найти значение функции в точке 
. 
отсюда 
или 
(9).
Пример1. Вычислить приближено 
.
Решение. Пусть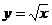 
; =36. Тогда 
. Подставляя полученные значения в формулу (8) получим 
. Итак 
.
Заключение.
Определение дифференциала как главной линейной части прираще-ния чрезвычайно важно, так как именно на нем основаны все важнейшие применения дифференциала. Как мы увидим дальше, в случае функций нес-кольких переменных существование производных и существование главной линейной части приращения не являются уже равнозначными требованиями; и весьма замечательно, что наиболее естественным определением дифферен-цируемости функции там оказывается, как мы увидим, не существование производных, а именно существование главной линейной части приращения.
Отыскание дифференциала данной функции, так же как и отыскание ее производной, называется дифференцированием этой функции. То, что этим двум операциям присваивается одно и то же наименование, естествен-но и понятно: если производная у’ найдена, то для получения дифференци-ала dy достаточно умножить ее на данное число ∆ х, задаваемое совершенно отдельно и независимо от х, что, очевидно, никаких новых аналитических расчетов уже не требует.
