Кривые второго порядка: окружность, эллипс, гипербола, парабола, вывод их канонических уравнений, исследование формы кривых, эксцентриситет и директрисы

I) Окружность -множество всех точек плоскости, равноудаленных от данной точки, называемой центром окружности.

 

 

Нормальное уравнение окружности

II) Эллипс -множество точек плоскости, для которых сумма расстояний до двух данных точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

- Каноническое уравнение эллипса

 

Эксцентриситетом эллипса называется отношение , где - половина расстояния между фокусами (a - бОльшая полуось)

Если 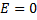, то получаем окружность

Директрисой эллипса называется прямая, параллельная его малой полуоси и отстоящая от неё на расстояние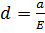

 

 

III) Гипербола -множество всех точек плоскости, для которых модуль разности расстояний до двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами

- каноническое уравнение гиперболы

Гипербола симметрична относительно обеих осей координат и относительно точки начала координат.

Эксцентриситетом гиперболы являются прямые, параллельные мнимой оси, проходящие на расстоянии 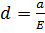от неё.

Гипербола имеет две асимптоты

Эксцентриситет определяет форму гиперболы: чем ближе эксцентриситет к нулю, тем ближе гипербола к окружности.

 

 

IV) Парабола

Каноническое уравнение параболы

 

Парабола не имеет асимптот. Осью симметрии является ох.

Вершина в т.О.