Уравнение поверхности, плоскость как поверхность второго порядка, общее уравнение плоскости и его исследование

Общее уравнение плоскости: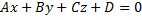

Уравнение плоскости в отрезках, уравнение плоскости, проходящей через три данные точки.

Уравнение плоскости в отрезках: , где

Уравнение плоскости, проходящей через три данные точки:

 

Нормальное уравнение плоскости, приведение общего уравнения плоскости к нормальному виду, расстояние от точки до плоскости.

Нормальное уравнение плоскости:

Общее уравнение плоскости может быть приведено к нормальному виду, умножением его на нормирующий множитель . Знак множителя берется противоположным знаку числа D

Нахождение расстояния от точки до плоскости:

Условия параллельности и перпендикулярности плоскостей.

Условие ||:

Условие ⏊:

 

Прямая линия в пространстве, различные виды её уравнений.

Векторно-параметрическое уравнение прямой:

Каноническое уравнение прямой:

Уравнения прямой по двум точкам:

Условия параллельности и перпендикулярности прямых в пространстве, условия параллельности и перпендикулярности прямой и плоскости.

Если прямые заданы уравнениям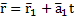и и 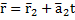, то они:

1) параллельны (но не совпадают)

2) совпадают

3) пересекаются

4) скрещиваются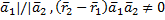

Условие ⏊ прямой и плоскости:

Условие || прямой и плоскости: