Цель: формирование умения вычислять пределы функций, раскрывая неопределенности и используя замечательные пределы.
Задание для самостоятельной внеаудиторной работы: 
& 12.1.Выучите определение предела функции в точке. Выясните, когда при вычислении пределов функции в точке возникает неопределенность вида 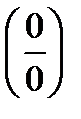 и в чем заключается техника ее раскрытия.
и в чем заключается техника ее раскрытия.
?12.2. Вычислите предел функции в точке:
а) 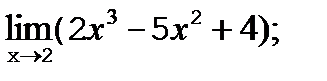 | б) 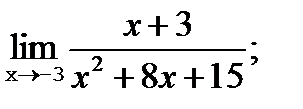 |
в) 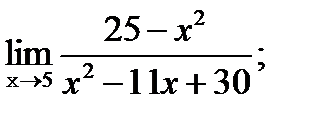 | г) 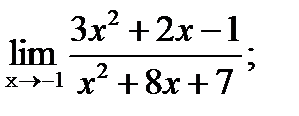 |
д) 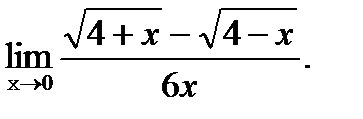 |
& 12.3.Выучите определение предела функции на бесконечности. Выясните, когда при вычислении пределов функции возникает неопределенность вида 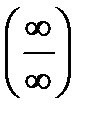 и в чем заключается техника ее раскрытия.
и в чем заключается техника ее раскрытия.
?12.4. Вычислите предел функции на бесконечности:
а) 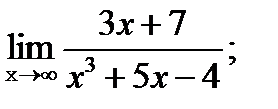 | б) 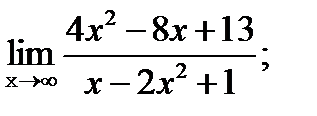 |
в) 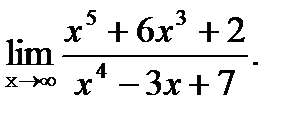 |
& 12.5.Запомните, какие пределы называются замечательными и проанализируйте, как они используются для вычисления пределов.
?12.6. Вычислите предел функции с помощью замечательных пределов:
а) 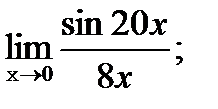 | б) 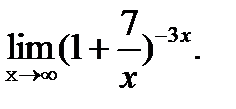 |
¶ 12.7. Вычислите предел функции:
а) 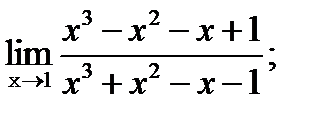 | б) 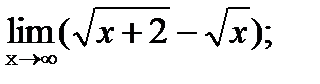 |
в) 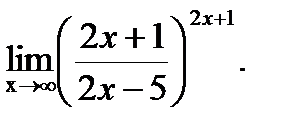 |
¶ 12.8. Выясните, при каком значении параметра 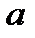
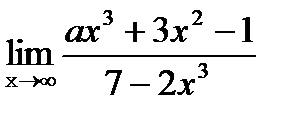 будет равен -1; 0;
будет равен -1; 0;  .
.
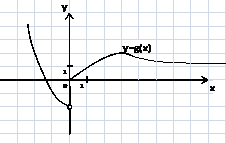
?12.9. Найдите предел функции, заданной графически, в указанных точках или на бесконечности:
|
 |
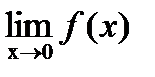 ,
, 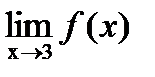 ,
, 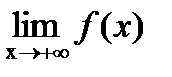 ,
, 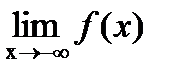
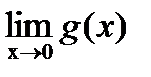 ,
, 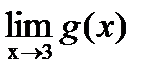 ,
, 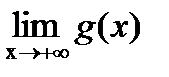 ,
, 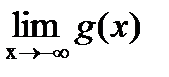
Методические указания по выполнению работы:
При решении задач необходимо знание следующего теоретического материала:
1. Предел функции в точке. Вычисление пределов путем раскрытия неопределенности вида 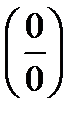 .
.
Число b называется пределом функции 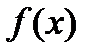 при х, стремящемся к хо (или в точке хо), если для любого наперед заданного
при х, стремящемся к хо (или в точке хо), если для любого наперед заданного 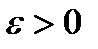 существует такое
существует такое 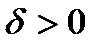 , что для всех х, удовлетворяющих условиям
, что для всех х, удовлетворяющих условиям 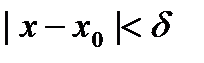 ,
, 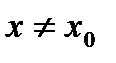 , имеет место неравенство:
, имеет место неравенство: 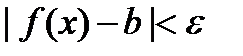 .
.
Если b есть предел функции 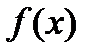 при
при 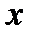 →
→ 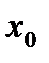 то пишут:
то пишут: 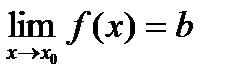 .
.
При вычислении предела функции в точке удобно использовать следующую технику:
1. Если под знаком предела стоит многочлен, то предел вычисляется простой подстановкой.
Пример 1. Вычислите: 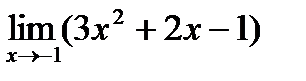 .
.
Решение. Подставим в многочлен вместо х значение -1, тогда
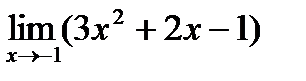 =
= 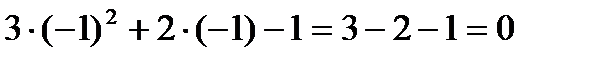 .
.
Ответ: 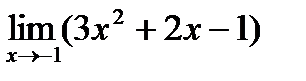 =0.
=0.
2. Если под знаком предела стоит отношение двух многочленов 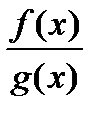 , то проверяем, обращается ли при подстановке хо знаменатель в ноль. Если не обращается, то предел вычисляется простой подстановкой.
, то проверяем, обращается ли при подстановке хо знаменатель в ноль. Если не обращается, то предел вычисляется простой подстановкой.
Если при подстановке хо знаменатель обращается в ноль, то необходимо использовать дополнительные приемы.
Если 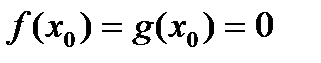 , то имеем неопределенность вида
, то имеем неопределенность вида 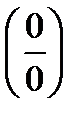 . В этом случае предел
. В этом случае предел 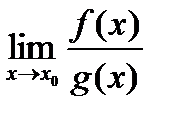 можно вычислить разложением многочленов
можно вычислить разложением многочленов 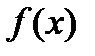 и
и 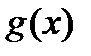 на множители, используя формулы сокращенного умножения и формулу разложения квадратного трехчлена на множители:
на множители, используя формулы сокращенного умножения и формулу разложения квадратного трехчлена на множители:
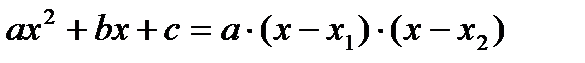 , где х 1 и х 2 – корни уравнения
, где х 1 и х 2 – корни уравнения 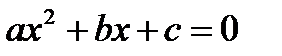 .
.
Если разложение выполнено верно, то в числителе и знаменателе дроби должны получиться одинаковые множители, которые следует сократить. После сокращения предел вычисляется простой подстановкой.
Пример 2. Вычислите 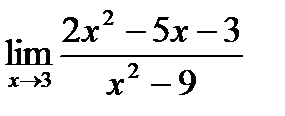 .
.
Решение. Проверим, какие значения будут принимать числитель и знаменатель при подстановке вместо х значения 3: 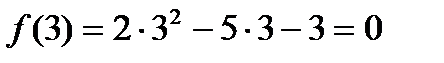 ,
, 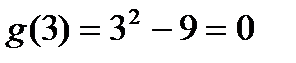 . Получили неопределенность вида
. Получили неопределенность вида 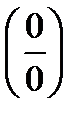 .
.
Разложим числитель на множители по формуле разложения квадратного трехчлена. Составим уравнение 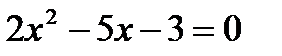 и найдем его корни:
и найдем его корни:
D = 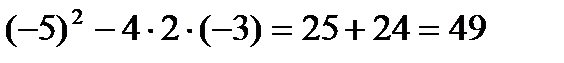 ;
;
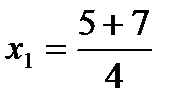 ;
; 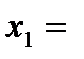 3 или
3 или 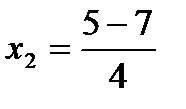 ;
; 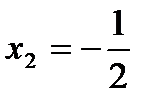 .
.
Тогда числитель можно представить в виде произведения двух множителей: 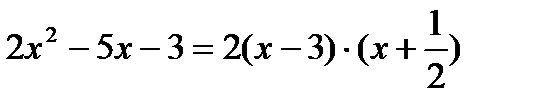 =
= 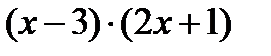
Знаменатель 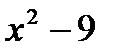 разложим по формуле разности квадратов:
разложим по формуле разности квадратов: 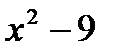 =
= 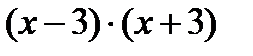 .
.
Вернемся к исходному пределу:
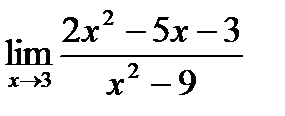 =
= 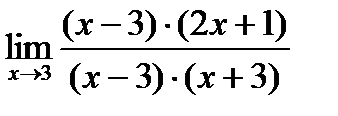 =
= 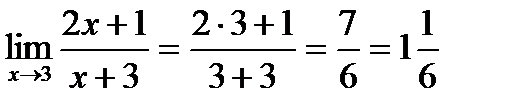 .
.
Ответ: 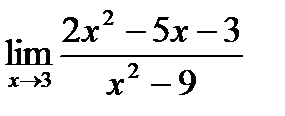 =
= 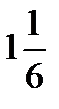 .
.
3. Если под знаком предела стоит дробь вида 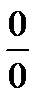 , включающая иррациональную функцию (функцию, содержащую корень), то домножаем числитель и знаменатель дроби на выражение, сопряженное иррациональному.
, включающая иррациональную функцию (функцию, содержащую корень), то домножаем числитель и знаменатель дроби на выражение, сопряженное иррациональному.
Пример 3. Вычислите 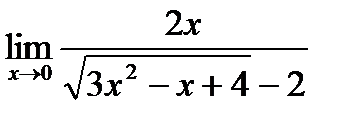 .
.
Решение. Поскольку при подстановке в числитель и знаменатель вместо х значение 0, получаем неопределенность вида 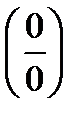 , домножим числитель и знаменатель дроби на выражение
, домножим числитель и знаменатель дроби на выражение 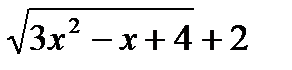 , сопряженное знаменателю. Получим:
, сопряженное знаменателю. Получим:
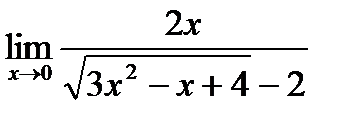 =
= 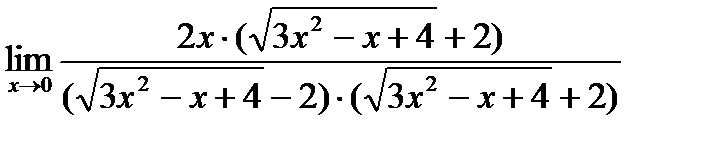 .
.
В знаменателе дроби воспользуемся формулой разности квадратов:
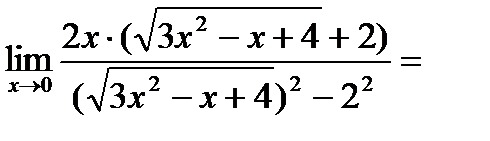
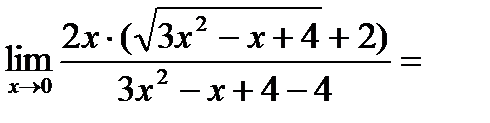
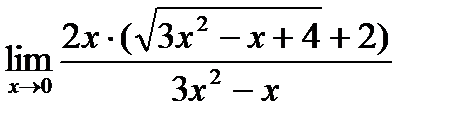 .
.
Вынесем в знаменателе х за скобки 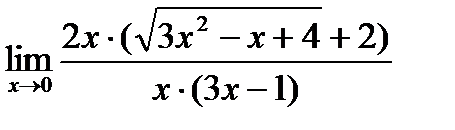 и сократим дробь на х:
и сократим дробь на х: 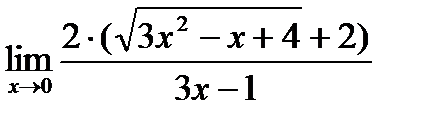 .
.
Видим, что при подстановке х =0 числитель и знаменатель не обращаются в 0, следовательно, теперь предел вычисляется простой подстановкой:
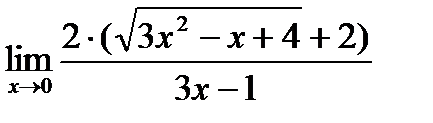 =
= 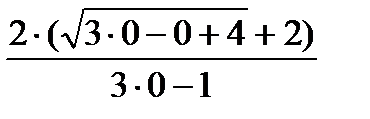 =
= 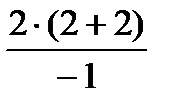 =-8.
=-8.
Ответ: 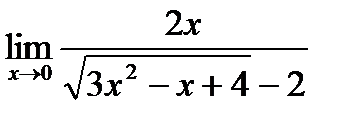 =-8.
=-8.
2. Предел функции на бесконечности. Вычисление пределов путем раскрытия неопределенности вида 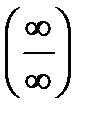 .
.
Число b называется пределом функции 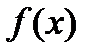 при
при 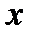 →∞, если для любого наперед заданного
→∞, если для любого наперед заданного 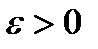 существует такое
существует такое 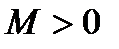 , что для всех
, что для всех 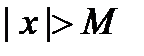 имеет место неравенство:
имеет место неравенство: 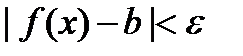 .
.
Если b есть предел функции 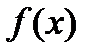 при
при 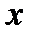 →∞, то пишут:
→∞, то пишут: 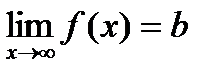 .
.
Для нахождения пределов функций на бесконечности часто используют два основных предела: 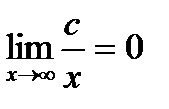 и
и 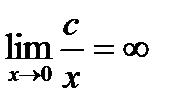 , где с – константа.
, где с – константа.
При вычислении предела дроби при 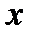 →∞ возникает неопределенность вида
→∞ возникает неопределенность вида 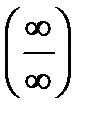 .Техника ее раскрытия заключается в том, что каждое слагаемое числителя и знаменателя нужно разделить на х в наивысшей степени. Возможны три случая:
.Техника ее раскрытия заключается в том, что каждое слагаемое числителя и знаменателя нужно разделить на х в наивысшей степени. Возможны три случая:
1)наивысшая степень числителя совпадает с наивысшей степенью знаменателя:
Пример 4. Вычислите 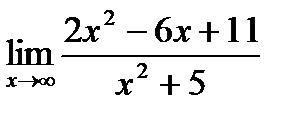 .
.
Решение. Разделим каждое слагаемое числителя и знаменателя на х2. Получим:
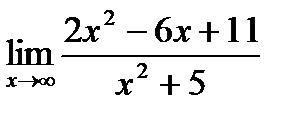 =
= 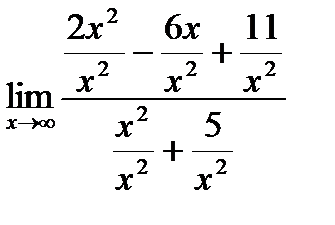 =
= 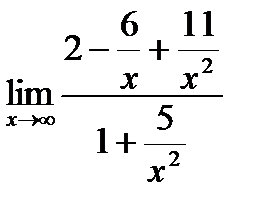 ;
;
Каждое слагаемое 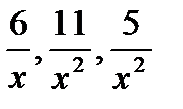 стремится к 0 при
стремится к 0 при 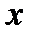 →∞, тогда
→∞, тогда
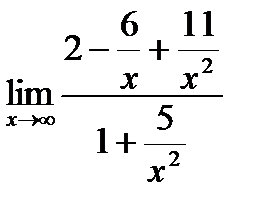 =
= 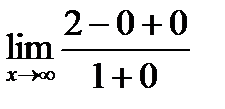 =2.
=2.
Ответ: 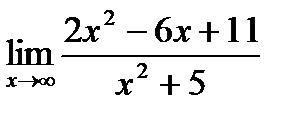 =2.
=2.
Итак, если наивысшая степень числителя совпадает с наивысшей степенью знаменателя, то в пределе получается число, отличное от нуля.
Пример 5. Вычислите 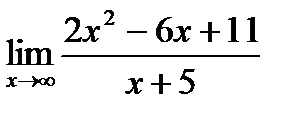 .
.
Решение. Разделим каждое слагаемое числителя и знаменателя на х2. Получим:
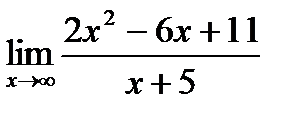 =
= 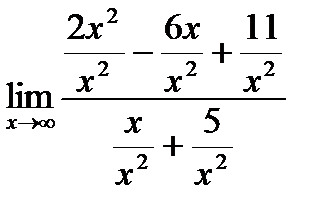 =
= 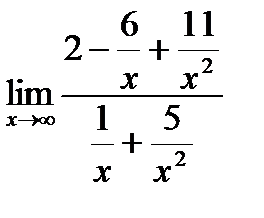 =∞.
=∞.
Ответ: 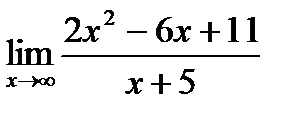 =
= 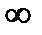 .
.
Таким образом, если наивысшая степень числителя больше наивысшей степени знаменателя, то в пределе получается бесконечность.
3)наивысшая степень числителя меньше наивысшей степени знаменателя:
Пример 6. Вычислите 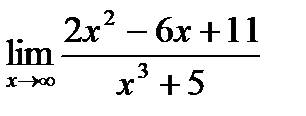 .
.
Решение. Разделим каждое слагаемое числителя и знаменателя на х3. Получим:
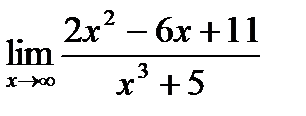 =
=  =
= 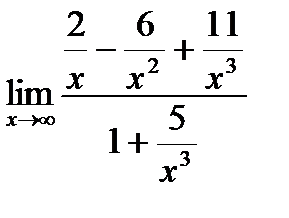 =
= 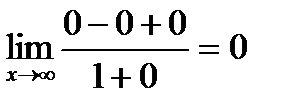 .
.
Ответ: 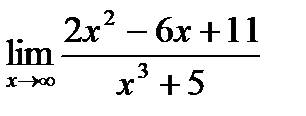 =0.
=0.
Таким образом, если наивысшая степень числителя меньше наивысшей степени знаменателя, то в пределе получается ноль.
 2015-04-01
2015-04-01 4590
4590