Позначимо номінальну вартість облігації або номінал через N. Його привласнюють облігації в момент її емісії. З часом ціна облігації може мінятися, але звичайно говорять не про ціну облігації Р, а про відношення ціни до номіналу і це відношення, виражене у процентах, називають курсом облігації К.
Таким чином, курс облігації визначається за формулою:
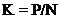 (8.1)
(8.1)
або у процентах
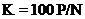 (8.2)
(8.2)
Облігації можуть мати купон, що характеризується купонною ставкою q, що дає власникові купонний доход, дорівнює частці q від номіналу.
Наприклад, якщо q = 10%, а N = 1000г.о., то разовий купонний доход дорівнює 100 г.о. Купонний доход виплачується періодично або тільки один раз, наприклад, при погашенні облігації, що обмовляється при покупці. Купонний доход розглядається як поточний.
Часто облігації мають установлений період дії, по закінченні якого вони можуть бути погашені. При погашенні власник одержує їхню номінальну вартість.
Облігації звичайно називаються по імені їхнього емітента: державні, якщо їх випустила держава, муніципальні, корпоративні і т. п.
Завдяки фіксованому поточному доходові облігації є досить популярними цінними паперами і по своїй вартості звичайно перевершують інші цінні папери.
Відзначимо для подальшого, що прибутковість облігації є її внутрішня прибутковість, що розуміється в значенні потоку платежів і обумовлена номіналом облігації в значенні сучасної або нарощеної величини. Ціна ж залежить і від зовнішніх умов, зокрема, від ставки процента.
Доход від такої облігації одержують тільки у вигляді купонних процентів. Якщо ставка купона q, ставка процента і, номінал облігації N, токупонні виплати, рівні 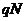 , утворять вічну ренту.
, утворять вічну ренту.
Застосовуючи знання по вищих фінансових вирахуваннях і дисконтуючи всі ці виплати по процентній ставці і, одержимо сучасну величину цієї ренти, що є теоретичною ціною облігації Р.
Таким чином,
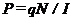 , (8.3)
, (8.3)
а курс облігації дорівнює
 . 8.4)
. 8.4)
Якщо виплата купонних грошей відбувається р раз у році у виді величини 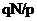 , так що за рік виходять ті ж
, так що за рік виходять ті ж 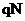 , то ці купонні виплати
, то ці купонні виплати 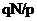 треба дисконтувати по ставці
треба дисконтувати по ставці 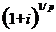 .
.
Тоді одержуємо формулу:
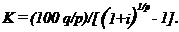 (8.5)
(8.5)
Тут проглядається аналогія з номінальною процентною ставкою.
Припустимо тепер, що курс облігації К відомий. Знайдемо поточну прибутковість облігації зазначеного типу. Якщо купонні виплати здійснюються один раз у рік, то за рік облігація приносить доход 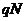 , а тому що в неї вкладено Р коштів, то, прибутковість дорівнює
, а тому що в неї вкладено Р коштів, то, прибутковість дорівнює
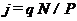 , (8.6)
, (8.6)
або, оскільки  ,
,
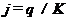 , (8.7)
, (8.7)
якщо курс вважати часткою, а у процентах −
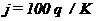 (8.8)
(8.8)
Можна запропонувати й інший спосіб визначення прибутковості облігацій зазначеного типу. Нехай прибутковість облігацій дорівнює j, тоді купонні виплати нарощують вартість облігації по цій річній ставці. Виходить, якщо дисконтувати цей потік по ставці j, то одержимо сучасну величину цього потоку, а це і є уже відома ціна облігації.
Купонні виплати являють собою вічну ренту, її сучасна величина дорівнює 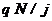 . Тому маємо рівняння
. Тому маємо рівняння
 , (8.9)
, (8.9)
звідки
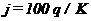 (8.10)
(8.10)
Таким чином, для облігацій розглянутого типу поточна і внутрішня прибутковості збігаються.
 2018-01-08
2018-01-08 272
272








