Плотность распределения непрерывной случайной величины и ее свойства

Плотностью распределения вероятности f(x) непрерывной случайной величины Х называют предел если он существует, отношение вероятности попадания случайной величины Х в интервале (x;x+ 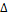х), примыкающий к точке х, к длине этого интервала, когда последняя стремится к 0.

Свойства:

1.f(x) неотрицательная функция т.к предел неотрицательных величин есть функция неотрицательная.

2.Вероятность попадания НСВ Х на промежуток [a,b] равна определенному интегралу по промежутку [a,b] от плотности распределения вероятностей.

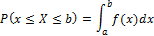
3.Вероятность достоверного события равна =1(вероятность того что св примет значение из (-

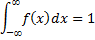
Если все возможные значение случайной величины принадлежат интервалу (a,b) то для f(x) ее плотности распределения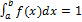

Плотность распределения может служить любая интегрируемая функция f(x) удовлетворяющая двум условиям f(x)>=0 и

Связь между функцией распределением и плотнотност и распределения вероятностей.

Функция F(х), которая определяется равенством F(х) = Р(Х х), называется интегральной функцией распределения или просто функцией распределения случайной величины X. Непосредственно из определения следует равенство

f(x)=F’(x) Плотность распределения f(x) называют дифференциальной функцией распределения.