Расположение прямой линии на координатной плоскости

Выясним особенности в расположении прямой относительно системы координат, если её общее уравнение

имеет неполный вид.

1) a=0 (b≠0). В этом случае уравнение прямой можно переписать так:

Все точки прямой имеют постоянную ординату. Следовательно, прямая горизонтальна.

y

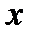
В частности, если и c=0, то уравнение прямой , а прямая совпадает с осью .

2) b=0 (a≠0). Этот случай рассматривается аналогично: Прямая вертикальна. Если и c=0, то x=0 - ось .

3) c=0. Уравнение (1) упрощается а прямая проходит через начало координат О(0,0), так как его координаты удовлетворяют этому уравнению.

4) a≠0, b≠0, c≠0. Уравнение (1) имеет полный вид, т.е. прямая не проходит через начало О и не параллельна ни оси x, ни оси . Преобразуем уравнение (1): 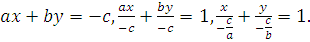Положим

Коэффициенты уравнения (2) имеют простой смысл: и с точностью до знака равны длинам отрезков, которые прямая отсекает на осях координат.

Уравнение (2) называется уравнением прямой в отрезках.

Упражнение 10. Задан пучок прямых .

Выяснить, что это такое, каковы значения параметра λ, при каких значениях λ прямая пучка параллельна оси , оси , проходит через начало координат, совпадает с базисными прямыми.

Уравнение прямой с угловым коэффициентом. Угол между прямыми.