Условия параллельности и перпендикулярности прямых

Пусть общее уравнение невертикальной прямой, тогда b≠0.

Положим

получим

Это известное уравнение невертикальной прямой с угловым коэффициентом k. Коэффициенты уравнения (2) имеют простой геометрический смысл: , угол, образуемый прямой с осью x, с точностью до знака длина отрезка, отсекаемого прямой на оси y.

 

 

y₂ А₂

А₁ y₂ y₁

y₁

 

В самом деле, пусть A₁(x₁, y₁), A₂(x₂, y₂) – две точки на прямой (2). Тогда

Ордината точки пересечения прямой и оси y находится легко:

Пусть на плоскости даны две невертикальные прямые

Угол между ними определяется формулой

Замечание. Если, например, вторая прямая вертикальна, то для неё не существует уравнения с угловым коэффициентом, но можно положить тогда по преобразованной формуле (4)

Пусть имеем две прямые, заданные общими уравнениями

Выясним, каким условиям должны удовлетворят коэффициенты уравнений прямых, чтобы они были: а) параллельны; б) перпендикулярны.

Допустим, что прямые невертикальны, тогда их уравнения можно записать в форме (3), где согласно обозначению (1)

Принимая во внимание формулу (4) для угла между параллельными прямыми, получим

Это очевидное условие параллельности, которое подходит и для вертикальных прямых.

Пусть невертикальные прямые (3) перпендикулярны, т.е. тогда по формулам (4)

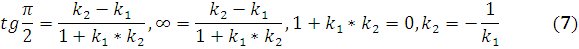
Нашли условие перпендикулярности.

Подставим обозначения (6) в условие (7):

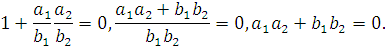
Получили условие перпендикулярности прямых, заданных общими уравнениями (5).