2017-11-01
672
Пусть на плоскости введены две системы координат 
с общим началом O. Связь между координатами точки A относительно этих систем координат определяется формулами
A
α 
E C
α
B D 
Эти формулы выражают координаты точки A в исходной системе координат 
через ее координаты в новой системе координат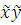 
. Отметим, что формулы (1) остаются справедливыми при любом расположении точки A на плоскости.
Пусть требуется найти каноническое уравнение кривой, которая задана в системе координат неканоническим уравнением
Сначала перенесём параллельно систему координат 
в точку 
, в результате чего получится система 
В качестве точки 
выбирается центр эллипса, гиперболы, либо вершина параболы. Координаты точек при параллельном переносе связаны формулами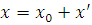 
, 
Подставляя их в уравнение (2), найдём уравнение кривой относительно системы координат 
Далее, поворачивая систему координат на угол 
, получим систему координат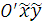 
, в которой согласно формулам (1) уравнение (3) принимает вид:
Это уравнение приводится к каноническому виду:
Технически угол выбирается так, чтобы в уравнении (4) отсутствовало произведение 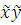. Каноническое уравнение (5) можно получить иначе, если сначала повернуть систему координат, а потом совершить параллельный перенос.
