2017-11-01
2680
Коническим сечением называется кривая, по которой пересекает круговой конус плоскость, не проходящая через его вершину.
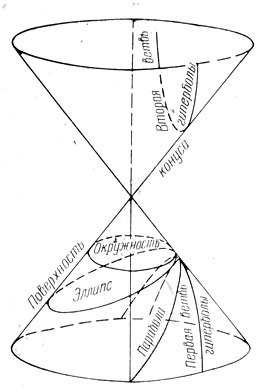
Каждое коническое сечение, кроме окружности, представляет собой геометрическое место точек плоскости, отношение расстояний от которых до некоторой точки F и прямой 
постоянно. Точка F называется фокусом конического сечения, а прямая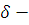 
директрисой.
Докажем это свойство. Пусть 
кривая, по которой плоскость 
пересекает плоскость. Впишем в конус сферу, касающуюся плоскости , и обозначим буквой F точку касания.
F
M
A B
Пусть 
плоскость, в которой лежит окружность касания сферы с конусом. Возьмём на кривой 
произвольную точку M. Опустим из неё два перпендикуляра:
1) на плоскость 
, длину которого обозначим 
;
2) на прямую 
основание которого обозначим A.
Проведём через точку 
образующую конуса и обозначим через B точку её пересечения с плоскостью . Наконец, пусть 
, 
угол между образующей конуса и плоскостью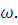 
Имеем, MF=FB, как касательные к сфере, проведённые из одной точки. Рассмотрим два треугольника с общим катетом длины :
|
|
|
что позволяет найти интересующее нас отношение
т.е. отношение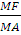 
не зависит от точки .
Обозначим отношение 
и назовём коническое сечние эллипсом (при 
), параболой (при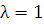 
) и гиперболой (при 
). Положительное число 
, часто обозначаемое 
, называется эксцентриситетом конического сечения.
Упражнение 17. Есть ли эксцентриситет у окружности? Как выглядят рисунки в случае параболы и гиперболы? Возможен ли другой рисунок для эллипса?
Пусть F 
фокус конического сечения , 
его директриса. В случае эллипса и параболы, когда λ 
все точки кривой 
располагаются по одну сторону от директрисы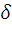 
, а именно где находится фокус F. Действительно, для всякой точки 
, расположенной с другой стороны директрисы, имеем 
что возможно лишь для точек гиперболы (), которая состоит из двух ветвей, разделённых директрисой.
Составим уравнения конических сечений в полярной системе координат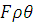 
, приняв за полюс фокус 
, а полярную ось проведём так, чтобы она была перпендикулярна директрисе 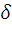и пересекала её.
Пусть 
расстояние от фокуса F до директрисы. Расстояние от произвольной точки M конического сечения до фокуса F есть полярный радиус 
, а расстояние от M до директрисы 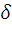равно 
, либо 
, смотря по тому, как располагаются точки M и F – по одну сторону от директрисы, либо по разные. Отсюда в случае эллипса и параболы получаем:
а для гиперболы, наряду с уравнением (1) может быть
Объединим их одной записью:
Одной ветви гиперболы соответствует знак «+», а другой – знак «–». Будем решать уравнение (1) относительно 
аналогично
|
|
|
= 
Это уравнение эллипса при и параболы при 
Уравнения ветвей гиперболы аналогичны:
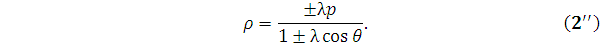
Проиллюстрируем изменение формы конического сечения в зависимости от эксцентриситета 
.
Замечание. В особых случаях пр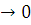и λ 
и λ 
имеем:
получили уравнение 
точки F, поэтому можно считать эксцентриситет точки 
;
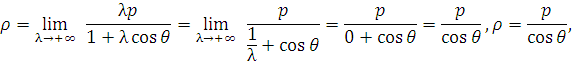
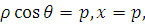
получили уравнение директрисы в декартовых координатах Fxy, поэтому можно считать эксцентриситетом прямой λ = + 
