Введём новые координаты x', y' по формулам

,

что соответствует параллельному переносу начала координат в точку O' (). Таким образом уравнение упростится:

Разделим на :

Введём обозначение

Разделим на :

Для эллипса поэтому положим

тогда уравнение (3) примет вид:

Это каноническое уравнение эллипса, которое рассматривалось в упражнении 4. Из обозначения (4) видно, что a>b, поэтому параметр a называют большой полуосью, b – малой полуосью эллипса.

Замечание 1. В особом случае λ=0 равенство (4) даёт a=b. Уравнение (5) принимает вид: Это уравнение окружности, поэтому эллипс обобщает окружность. Если a<b, то фокусы лежат на оси y.

Для гиперболы поэтому положим

тогда уравнение (3) примет вид:

Это каноническое уравнение гиперболы. Параметр называется действительной полуосью, а параметр b – мнимой полуосью гиперболы. Обозначение (6) показывает, что в случае полуоси равны a=b. Такая гипербола называется равнобокой или равносторонней.

Для параболы 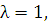поэтому уравнение (2) упрощается: