2017-11-01
755
Если точка 
принадлежит плоскости
,
то её координаты удовлетворяют уравнению (1). Выясним, какой геометрический смысл имеет выражение
,
если точка 
не принадлежит плоскости.
Опустим из точки 
перпендикуляр на плоскость. Пусть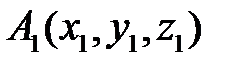 
- основание перпендикуляра. Так как точка 
лежит на плоскости, то 
. Выразим отсюда 
и подставим в выражение (2), получим:
где 
- вектор, перпендикулярный плоскости, 
– его модуль, 
- расстояние от точки 
до плоскости.; 
при 
; 
при 
. Получим
.
Таким образом, выражение (2) положительно для точек по одну сторону плоскости и отрицательно по другую.
Из равенства (3) следует:
,
т.е. по абсолютной величине выражение (2) пропорционально расстоянию 
с коэффициентом пропорциональности
.
Равенство (5) дает основную формулу для вычисления расстояния от точки 
до плоскости (1):
.
Если для коэффициентов уравнения выполняется равенство 
,т.е. вектор 
- единичный, то формула упрощается: 
. Значит, выражение (2) с точностью до знака равно расстоянию 
. В этом случае говорят, что уравнение плоскости (1) в нормальной форме. Можно увидеть, что тогда 
, где 
- углы, образованные единичным вектором 
с осями 
соответственно. Эти косинусы называются направляющими косинусами вектора 
и удовлетворяют равенству 
.
Чтобы получить нормальную форму из общего уравнения плоскости (1), достаточно разделить его на коэффициент 
: 
.
Оно с точностью до знака имеет вид: 
, куда входят направляющие косинусы неединичного вектора 
и расстояние 
от начала координат О до плоскости.
