 У ОХ - действительная ось,
У ОХ - действительная ось,

 bi z =а + bi ОУ – мнимая ось.
bi z =а + bi ОУ – мнимая ось.
 0 а х
0 а х
Пример:

 3i у 3+3i
3i у 3+3i

 -2+2i 2i
-2+2i 2i

 i 1+i
i 1+i


 -3 -2 -1 0 1 2 3 X
-3 -2 -1 0 1 2 3 X
-i
 -3-2i -2i
-3-2i -2i


 -3i 2-3i
-3i 2-3i
 Геометрический смысл модуля комплексного числа
Геометрический смысл модуля комплексного числа
у
Z z =а + bi 


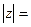
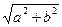 — расстояние от точки О до точки Z.
— расстояние от точки О до точки Z.
0 X
 Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа
У z = r(cos Ψ + i sin Ψ), где r = 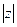 , т.е.
, т.е.


 bi z r =
bi z r = 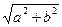
0  Ψ
Ψ
Итак, для того, чтобы комплексное число, заданное в алгебраической форме, обратить в тригонометрическую форму, необходимо найти его модуль r и аргумент j, пользуясь формулами:
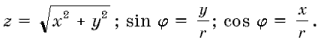
Пример: Дано 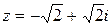 , записать тригонометрическую форму комплексного числа.
, записать тригонометрическую форму комплексного числа.
Решение:
Дано 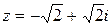 - алгебраическая форма.
- алгебраическая форма.
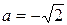 ,
, 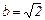 ,
, 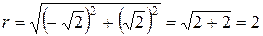 ,
,
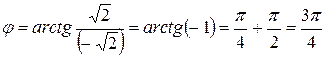 .
.
Формулы Муавра
Возведение в целую степень п. Модуль возводится в эту степень, аргумент умножается на п.
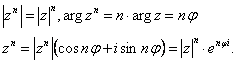 (1)
(1)
Извлечение корня степени п. Извлекается арифметический корень из модуля, общее значение аргумента делится на п. Корень имеет ровно п различных значений, если 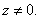
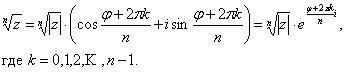 (2)
(2)
Формулы (1) и (2 называются формулами Муавра
Вопросы для самопроверки по теме 4 Основы теории комплексных чисел
1. Что называется комплексным числом?
2. Какие интерпретации комплексных чисел вы знаете? Опишите их.
3. Что называется действительной и мнимой частями комплексного числа?
4. Что называется алгебраической и тригонометрической формами комплексного числа?
5. В каком случае два комплексных числа называются сопряженными?
6. По каким правилам производятся арифметические действия над комплексными числами?
Тема 5 Теория вероятностей и математическая статистика.
Студент должен:
иметь представление:
- о случайных событиях и их вероятности;
- о функциях распределения случайных величин;
- о задачах математической статистики.
знать:
- определение вероятности событий;
- определения видов событий;
- определения операций над событиями;
- формулировки теорем сложения и умножения вероятностей;
- способы задания случайной величины;
- определения дискретной и непрерывной случайной величины;
- закон распределения вероятностей дискретной случайной величины;
- задачи математической статистики.
уметь:
- оценить по относительной частоте события вероятность его появления или не появления;
- находить вероятность события, пользуясь классическим определением вероятности и простейшими комбинаторными схемами;
- вычислять вероятности суммы несовместных событий, произведения независимых событий;
- строить ряд распределения;
- находить функцию распределения случайной величины;
- решать простейшие задачи.
Опыт. События. Виды событий. Случайные события. Виды случайных событий. Относительная частота появления события. Классическое определение вероятности события.
Операции над событиями. Теоремы сложения и умножения вероятностей.
Противоположные события. Повторные независимые испытания. Формула Бернулли.
Случайная величина. Функция распределения случайных величин.
Задачи математической статистики. Функции выборки. Некоторые важнейшие распределения. Случайная выборка, понятие генеральной совокупности.
 2017-11-01
2017-11-01 894
894

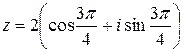 -
- 






