При элементарных преобразованиях ранг матрицы не изменяется

 

Пример 15. Привести матрицу А = 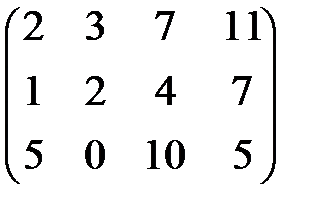к ступенчатому виду.

Решение. 1) Умножим элементы второй строки на 2 и вычтем их из соответствующих элементов первой строки и получим эквивалентную матрицу

В ₁ = .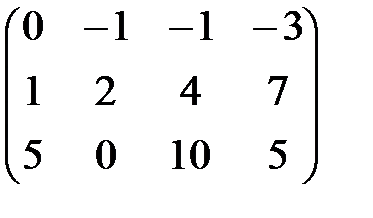

2) Умножим все элементы второй строки матрицы В ₁ на 5 и вычтем их из соответствующих элементов третьей строки, получим новую эквивалентную матрицу

В ₂ = .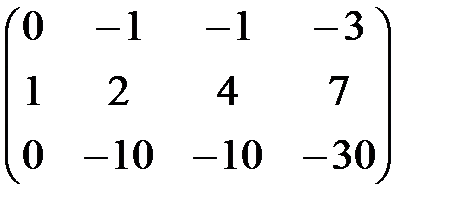

3) Поменяем местами первую и вторую строки

 

В ₃ = .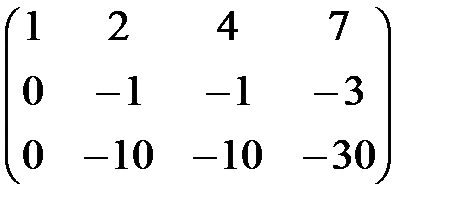

Замечаем, что элементы второй и третьей строк находятся в линейной зависимости.

4) Умножаем элементы второй строки на 10 и вычитаем их из соответствующих элементов третьей строки, получаем другую эквивалентную матрицу

В ₄ = .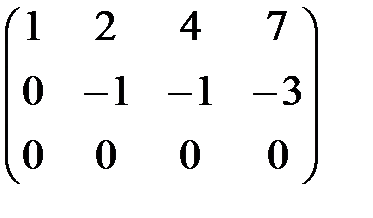

Полученная матрица В ₄ является ступенчатой и её ранг, как нетрудно видеть, равен r (B ₄) = r (A) = 2.

 

Ранг ступенчатой матрицы равен числу её ненулевых строк

 

Понятия обратной матрицы и ранга матрицы используются, в частности, при решении систем линейных алгебраических уравнений.

 

Вопросы для самопроверки

 

1. Какие матрицы называются равными, диагональными, транспонированными, симметрическими, перестановочными?

2. Сформулируйте свойства сложения матриц.

3. Сформулируйти правило умножения двух матриц. В чем состоит условиие, необходимое для существования произведения матриц?

4. Сформулируйте свойства умножения матриц.

5. Как определяется обратная матрица? В чем состоит условие, необходимое для существования обратной матрицы?

6. Какие существуют правила для вычисления определителей 3-го порядка?

7. Что называется минором некоторого элемента определителя 3-го (произвольного) порядка?

8. Что называется алгебраическим дополнением некоторого элемента определителя третьего (произвольного) порядка?

9. Напишите разложение определителя 3-го порядка по 3-й строке и по 3-му столбцу.

10. Сформулируйте свойства определителей.

11. Что называется рангом матрицы и как он вычисляется?