Определение поверхностного интеграла первого рода

Пусть G - гладкая (кусочно-гладкая) ограниченная поверхность, в каждой точке которой определена функция 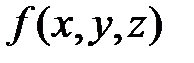. Разобьём произвольным образом поверхность на 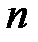частей 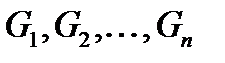, площади которых 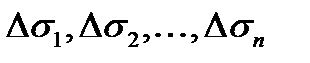. Выберем на каждой из частей произвольную точку 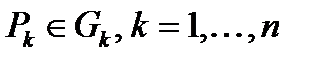и составим интегральную сумму .

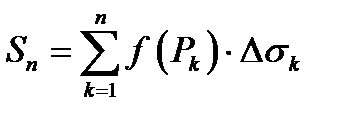Если существует предел последовательности интегральных сумм при неограниченном увеличении числа разбиений и уменьшении каждой части, то этот предел называется поверхностным интегралом первого рода. .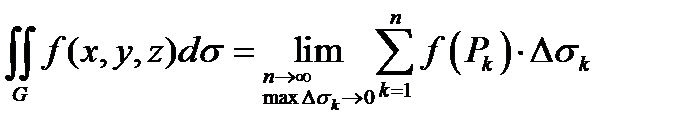

Теорема существования. Если функция 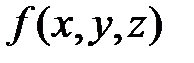непрерывна в каждой точке гладкой поверхности 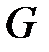, то она интегрируема по этой поверхности, т.е. существует предел последовательности интегральных сумм, который не зависит от способа разбиения поверхности на части и от выбора точек.