Вычисление поверхностного интеграла 1-ого рода

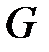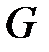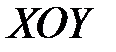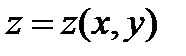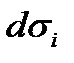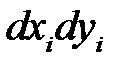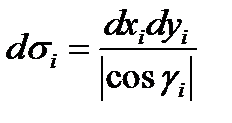Вычисление поверхностного интеграла сводится к вычислению двойного интеграла по той области, которая получается при проецировании поверхности на одну из координатных плоскостей. Если поверхность однозначно проецируется на координатную плоскость и её уравнение можно представить в виде , то каждая элементарная часть проецируется в элементарную площадку и , где 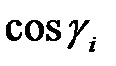- аппликата единичного вектора, перпендикулярного касательной плоскости к поверхности в точке 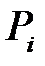, причём 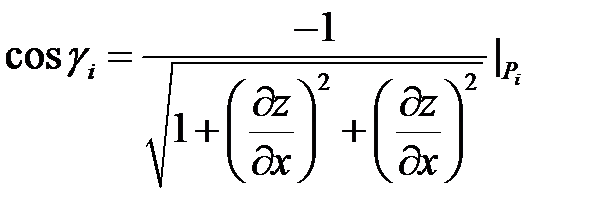. (См. занятие 3, часть 2)

Тогда .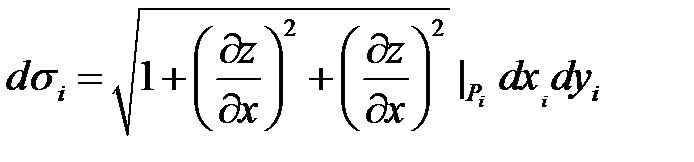

При этом поверхностный интеграл вычисляется по формуле:

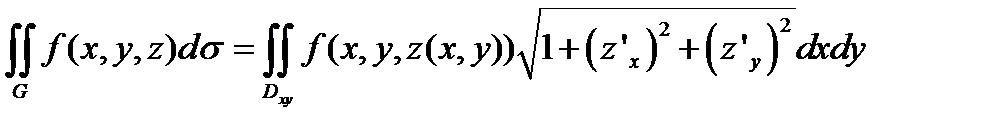, (12.1)

где 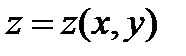- уравнение поверхности G.

Если поверхность 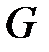удобнее спроецировать на координатную плоскость 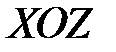, то

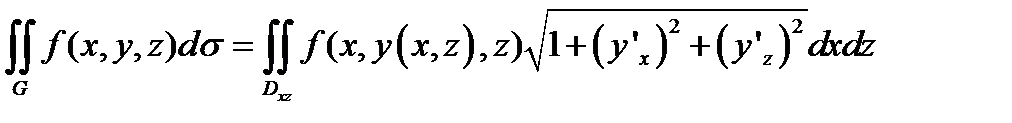, (12.2) где 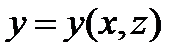- уравнение поверхности G.

И аналогично, при проецировании на 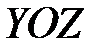имеем

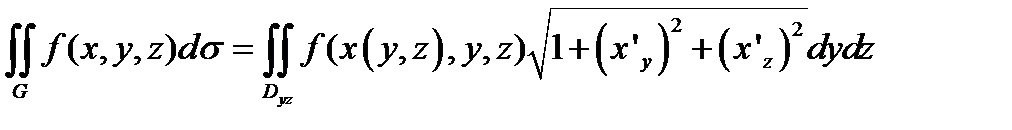, (12.3) где 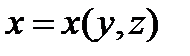- уравнение поверхности G.

3 .Свойства поверхностного интеграла первого рода.

1) Свойство линейности:

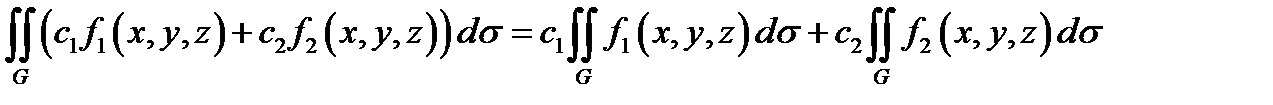2) Свойство аддитивности:

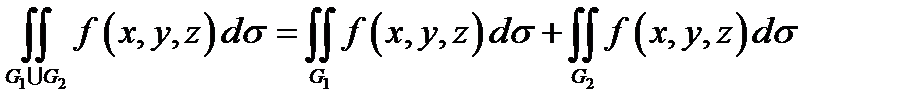
3) Теорема о среднем. Если 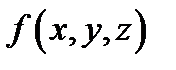непрерывна на поверхности G, то существует число ζ такое, что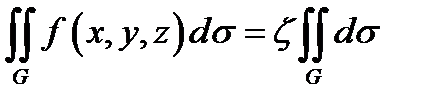

4) Теорема об оценке. Если числа M и m - соответственно наибольшее и наименьшее значения функции 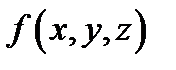на поверхности G, то верно неравенство: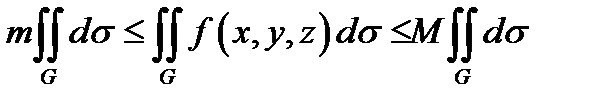

5) Криволинейный интеграл от единичной функции равен площади поверхности:

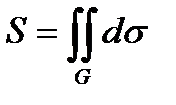. (12.4)

4.Некоторые приложения поверхностного интеграла 1-ого рода.

1) Масса материальной поверхности переменной плотности 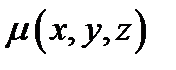может быть найдена по формуле

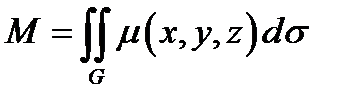. (12.5)

2)Координаты центра масс материальной поверхности :

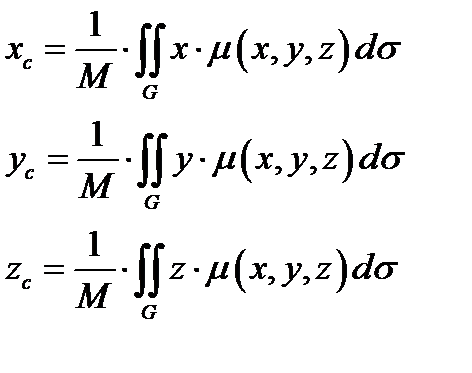(12.6)

3)Моменты инерции поверхности относительно осей координат:

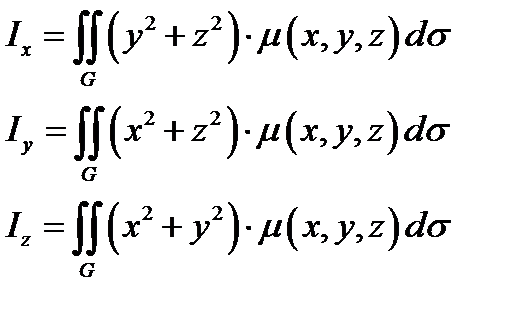(12.7)

4) Момент инерции поверхности относительно начала координат:

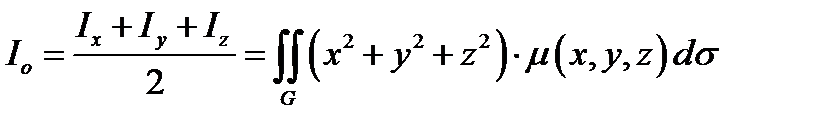(12.8)