Понятие гладкой поверхности. Ориентированная поверхность

Определение. Поверхность называется гладкой, если в каждой её точке существует касательная плоскость, непрерывно меняющаяся вдоль поверхности.

Если поверхность состоит из нескольких гладких частей, примыкающих друг к другу и не имеющих общих внутренних точек, то она называется кусочно-гладкой.

В каждой точке гладкой поверхности можно построить единичный нормальный вектор 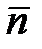, который непрерывно будет перемещаться вместе с перемещающейся касательной плоскостью.

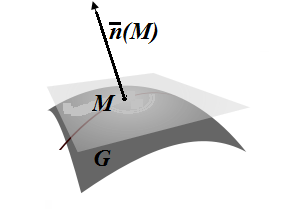
Рисунок 13.6

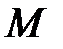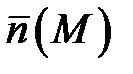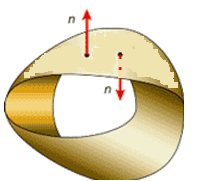
Возьмём на гладкой поверхности произвольную точку и зафиксируем нормальный вектор . Если при движении этой точки по какому-либо контуру, принадлежащему поверхности и не пересекающему её границы, точка может прийти в исходное положение так, что при этом нормальный вектор окажется противоположно направленным своему первоначальному положению, то эта поверхность называется односторонней.

Рисунок 13.7

Примером односторонней поверхности является «лист Мёбиуса» (см. рис. 13.1).

Если такая ситуация невозможна, поверхность называется двусторонней.

Определение. Двусторонняя гладкая поверхность называется ориентированной, если в некоторой её точке выбран один из двух возможных нормальный вектор так, чтобы он непрерывно менялся от точки к точке (см. рис. 13.2).

 

2.Определение поверхностного интеграла второго рода.

Пусть G - гладкая (кусочно-гладкая) ориентированная двусторонняя поверхность, в каждой точке которой определена функция 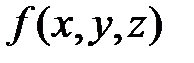. Разобьём произвольным образом поверхность на 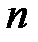частей 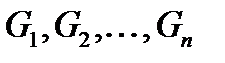, площади которых 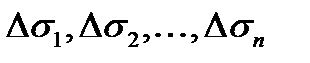. Выберем на каждой из частей произвольную точку 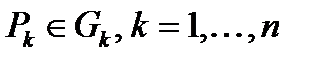. Пусть 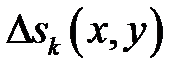- площадь проекции части 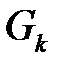на координатную плоскость 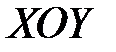, взятая со знаком «плюс», если выбранный вектор 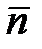составляет острый угол 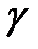с осью 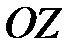, и со знаком «минус», если этот угол тупой. Составим интегральную сумму .

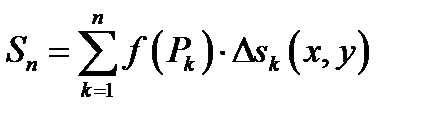Определение. Если существует предел последовательности интегральных сумм при неограниченном увеличении числа разбиений и уменьшении каждой части, то этот предел называется поверхностным интегралом второго рода по переменным 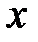и .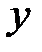

.

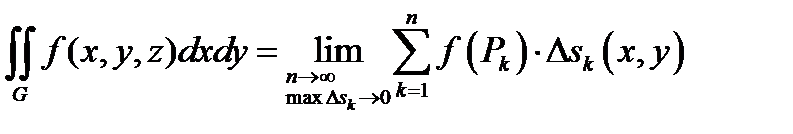Аналогично определяются поверхностные интегралы 2-ого рода по переменным 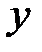и 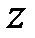, а также по 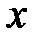и .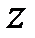

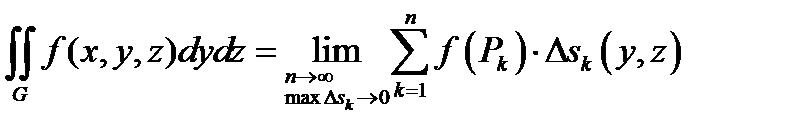
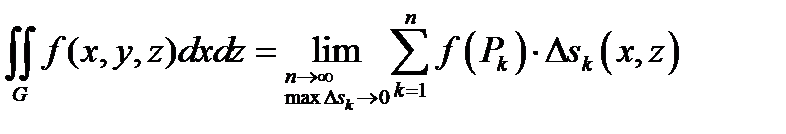
В общем случае поверхностный интеграл 2-ого рода выглядит следующим образом:

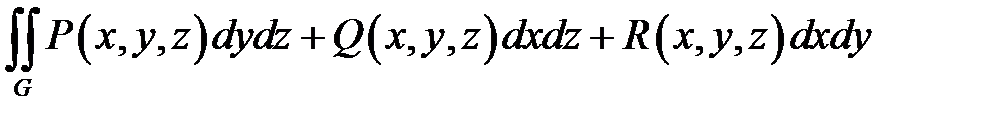(13.1)