2017-11-01
2854
Пусть σ – некоторая ориентированная поверхность в области G. Выберем определённую её сторону, задав единичный вектор нормали к поверхности 
.
Определение. Потоком вектора 
через поверхность σ называется поверхностный интеграл от скалярного произведения вектора поля на нормальный единичный вектор к поверхности: 
. (14.4)
Имеют место другие формы записи потока вектора. Например, учитывая, что 
, получим: 
. Или можно определить вектор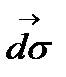 
, направленный по нормали к поверхности, такой, что: 
, 
. Тогда: 
.
Если поверхностьσзамкнута, то обычно за направление вектора 
берут направление внешней нормали к поверхности и обозначают
. (14.5)
Если изменить ориентацию (взять другую сторону поверхности), то скалярное произведение 
и, соответственно, поток меняют знак.
Поток можно записать в координатной форме, вычислив скалярное произведение векторов 
и 
:
. (14.6)
Или 
(см. занятие 13), (14.7)
где в правой части имеем поверхностный интеграл второго рода.
Пример 14.2. Вычислим поток векторного поля 
через часть плоскости 
, заключённую в первом октанте, в сторону нормали, составляющей тупой угол с осью OY.
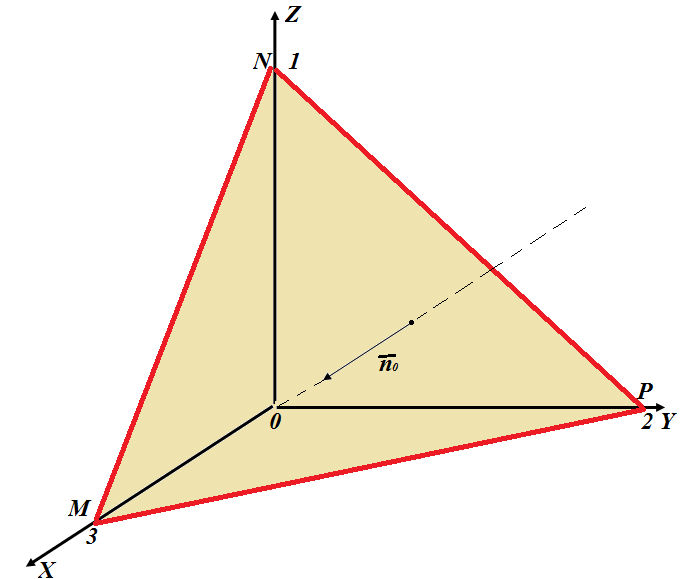
Решение. Вычислим поток по формуле (14.4): 
, где σ – плоскость с уравнением 
. (см. рис.14.3)
| Рисунок 9 |
является 
. | Рисунок 14.3 |
. Этот вектор составляет острый угол с осью OY. А единичный вектор, составляющий тупой угол с 
равен 
. Сведём задачу к вычислению интеграла I рода (см. занятие 13). Для этого вычислим скалярное произведение 
и подставим его в формулу.
, 
.
Но 
, т.е. 
. Из векторной алгебры известно, что площадь треугольника MNP равна половине модуля векторного произведения двух векторов, на которых построен треугольник (см. рис. 14.3), т.е. 
.
Ответ: 
.
Замечание. Можно было бы вычислить поток с помощью поверхностного интеграла 2-ого рода (см. (14.6) и (14.7)). Тогда каждое из слагаемых в формуле (14.7) преобразуется в двойной интеграл по области D, являющейся проекцией поверхности σ на соответствующую координатную плоскость(см.занятие13): 
