Векторные линии поля

Определение. Векторной линией векторного поля называется линия, в каждой точке которой вектор поля направлен по касательной к ней. (см. рис. 14.1)

В физике это понятие для конкретных полей имеет физический смысл, например, векторные линии поля тяготения, электрического и магнитного полей - это силовые линии, а поля скоростей – линии тока, т.е. линии, по которым движутся частицы поля.

Пусть векторная линия, проходящая через точку , имеет уравнение , где t – параметр. Из условия коллинеарности вектора касательной и вектора поля в произвольной точке векторной линии следует дифференциальное уравнение этой линии: , (14.1)

где λ – некоторое число.

Уравнение (14.1) - дифференциальное уравнение векторных линий в векторной форме.

В пространстве в декартовой системе координат для векторов

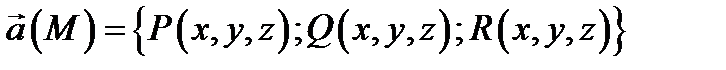и векторное уравнение (14.1) эквивалентно системе дифференциальных уравнений:

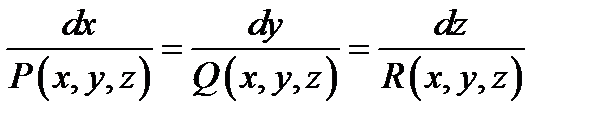, (14.2)

Система (3) – это симметричная форма системы дифференциальных уравнений. Для её решения применяются интегрируемые комбинации, с привлечением свойств равных дробей. Для плоского поля система превращается в одно уравнение:

. (14.3)

Определение. Поверхность, состоящая из векторных линий, проведённых через каждую точку некоторой замкнутой линии l, называется векторной трубкой.

Пример 14.1. Найдём векторныелинии векторного поля и построим их.

Решение. Поле, у которого 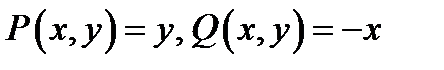, определено на всей плоскости XOY, следовательно, через каждую точку плоскости проходит хотя бы одна векторная линия. Составим дифференциальное уравнение векторных линий: (см. (14.3)). Это уравнение с разделяющимися переменными. Решим его: , или - уравнения векторных линий. При С=0 это точка О(0,0), при С>0 – концентрические окружности.

Для определения направления движения по векторной линии материальной точки, попавшей в векторное поле, рассмотрим проекцию вектора 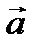на ось OX. Это . Там, где , 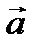составляет с осью OX острый угол, где - тупой. Учитывая, что вектор поля направлен по касательной к векторной линии, и векторные линии непрерывны, достаточно выяснить,

что в первой четверти движение поля происходит по часовой стрелке (см. рис. 14.2).

Ответ: - уравнения векторных линий.